


: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―II ïŋ―ïŋ―ïŋ―ïŋ― No.10
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

ïŋ―Ęēïŋ― 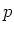 ïŋ―ïŋ―ïŋ―Įŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Įŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―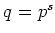 (
(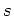 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
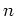 ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
 ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
 ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
 ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ïŋ― (
ïŋ―ïŋ―ïŋ―ëĪĪïŋ―ïŋ― (
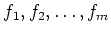 ïŋ―ïŋ―ïŋ―ïĪŦïŋ―ęĪïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―)
ïŋ―ïŋ―ïŋ―ïĪŦïŋ―ęĪïŋ―ÃĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―)
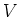 ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪđïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪđïŋ―ïŋ―
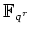 ïŋ―ĮĪïŋ―
ïŋ―ĮĪïŋ―
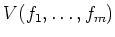 ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
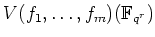 ïŋ―Į―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Į―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ― 10.1
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
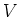
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
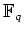
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏĄïŋ―
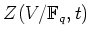
ïŋ―ĘĪÉĪČĪïŋ―ņĪŊĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïīïŋ―ĘŽïŋ―ïĪŦïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ξïŋ―ïŋ―ïŋ―  ïŋ―ïŋ―
ïŋ―ÂĪÏ·ïŋ―ĖĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĪŋïŋ―ïŋ―Îđïŋ―ïŋ―ŨĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÞĄïŋ―
ïŋ―ïŋ―
ïŋ―ÂĪÏ·ïŋ―ĖĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĪŋïŋ―ïŋ―Îđïŋ―ïŋ―ŨĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÞĄïŋ―
 ïŋ―ČĪĘĪïŋ―čĪĶïŋ―Ęđïŋ―ïŋ―ïŋ―
ïŋ―ČĪĘĪïŋ―čĪĶïŋ―Ęđïŋ―ïŋ―ïŋ―  ïŋ―ïŋ―
Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ïŋ―
Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―Čđïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―  ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŦïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îļïŋ―Íïŋ―ÍĪÏĪÉĪÎĪčĪĶïŋ―ĘĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ÜđÖĩïŋ―ïŋ―ĮĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―Ƨïŋ―ßđïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŦïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îļïŋ―Íïŋ―ÍĪÏĪÉĪÎĪčĪĶïŋ―ĘĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ÜđÖĩïŋ―ïŋ―ĮĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―Ƨïŋ―ßđïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―
2ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
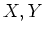
ïŋ―ËīØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
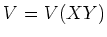
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
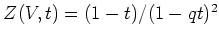
.
ïŋ―ïŋ―
2ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
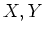
ïŋ―ËīØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
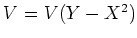
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
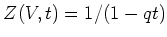
ïŋ―ïŋ―
2ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
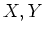
ïŋ―ËīØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
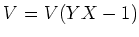
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
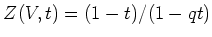
ïŋ―ïŋ―ïŋ―ïŋ― 10.1
3ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
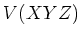
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 10.2
3ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
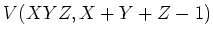
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 10.3
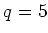
ïŋ―ČĪïŋ―ïŋ―ëĄĢ
2ïŋ―Ņŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
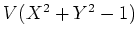
ïŋ―Îđïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―
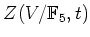
ïŋ―ïŋ―ïŋ―ČĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ŌĨïŋ―ïŋ―:
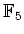 ïŋ―ËĪïŋ―
ïŋ―ËĪïŋ― 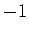 ïŋ―ïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ōĪĶĪÞĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―Ęŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ōĪĶĪÞĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―



: ïŋ―ïŋ―ïŋ―ïŋ―Ęļïŋ―ïŋ―ËĪÄĪïŋ―ïŋ―ïŋ―...
2002ĮŊ6ïŋ―ïŋ―25ïŋ―ïŋ―
![]()
![]() ïŋ―ïŋ―ïŋ―Įŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Įŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―![]() (
(![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢ
![]() ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
ïŋ―ÄĪïŋ―ïŋ―Ņŋïŋ―
![]() ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°
![]() ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![]() ïŋ―ĮĪïŋ―
ïŋ―ĮĪïŋ―
![]() ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―
![]() ïŋ―Į―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Į―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
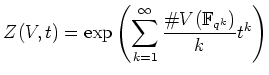
![]() ïŋ―ïŋ―
ïŋ―ÂĪÏ·ïŋ―ĖĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĪŋïŋ―ïŋ―Îđïŋ―ïŋ―ŨĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÞĄïŋ―
ïŋ―ïŋ―
ïŋ―ÂĪÏ·ïŋ―ĖĪïŋ―Íïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ëĪŋïŋ―ïŋ―Îđïŋ―ïŋ―ŨĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÞĄïŋ―
![]() ïŋ―ČĪĘĪïŋ―čĪĶïŋ―Ęđïŋ―ïŋ―ïŋ―
ïŋ―ČĪĘĪïŋ―čĪĶïŋ―Ęđïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―
Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
ïŋ―ïŋ―
Âļïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ÐĄïŋ―
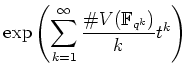
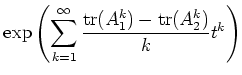
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŦïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îļïŋ―Íïŋ―ÍĪÏĪÉĪÎĪčĪĶïŋ―ĘĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ÜđÖĩïŋ―ïŋ―ĮĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―Ƨïŋ―ßđïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪŦïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îļïŋ―Íïŋ―ÍĪÏĪÉĪÎĪčĪĶïŋ―ĘĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĪŦïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōĪĪ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ÜđÖĩïŋ―ïŋ―ĮĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪïŋ―Ƨïŋ―ßđïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―
 ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―