


Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― II ïŋ―ïŋ―ïŋ―ïŋ― No.4
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:

ïŋ―ïŋ―ïŋ― 4.1
ïŋ―ïŋ―
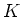
ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
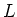
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĄïŋ―
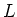
ïŋ―ïŋ―
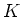
-ïŋ―ŲĨïŋ―ïŋ―ČĨïŋ―ïŋ―ïŋ―ÖĪČĪïŋ―ïŋ―ÆĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―
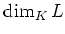
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
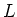
ïŋ―ïŋ―
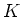
ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―įžĄïŋ―ïŋ―ïŋ―ČļÆĪÓĄïŋ―
![$[L:K]$](img5.png)
ïŋ―Į―ïŋ―É―ïŋ―ïŋ―ïŋ―ïŋ―
![$[L:K]<\infty$](img6.png)
ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
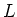
ïŋ―ïŋ―
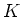
ïŋ―ïŋ―
Íïŋ―žïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČļÆĪÐĪïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ― 4.2
ïŋ―ïŋ―ïŋ―
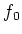
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
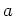
ïŋ―ïŋ―
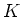
ïŋ―ïŋ―ΚĮūïŋ―Âŋïŋ―āž°ïŋ―ČļÆĪÖĄïŋ―
ïŋ―ïŋ―ïŋ―Îŧïŋ―ïŋ―ÂĪÏĪïŋ―ïŋ―ÎđÖĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ÎĪïŋ―ïŋ―ïŋ―ËĪïŋ―ÉŽïŋ―ÜĪïŋ―ïŋ―Ξïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïĪąïŋ―ĮĪÏĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―äĪđïŋ―ïŋ―ïŋ―ĘĪïŋ―ÎĪĮŧČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 4.1 (``ïŋ―ïŋ―ïŋ―ïŋ―ØĪÎīïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―'')
ĘĢïŋ―Įŋïŋ―ïŋ―ïŋ―
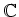
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
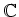
ïŋ―ïŋ―ïŋ―ĮĪïŋ―ÕĪÎĢïŋ―ïŋ―Ņŋïŋ―Âŋïŋ―āž°
(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ÉŽïŋ―ïŋ―
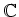
ïŋ―ÎĪĘĪïŋ―ïŋ―Ëšïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĢïŋ―Įēïŋ―ïŋ―ÏģØĪïŋ―ïŋ―ÎĪÃĪÆĪïŋ―ïŋ―ïŋ―ĘĪïŋ―Кïŋ―ïŋ―ïŋ―ïŋ―ÍĪÎļïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ÃĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― 4.1
ĘĢïŋ―Įŋïŋ―ïŋ―Îūïŋ―ïŋ―1ïŋ―Ņŋïŋ―
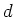
-ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―,ÉŽïŋ―ïŋ―
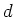
ïŋ―ÄĪΚïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĄïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Č°ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 4.1
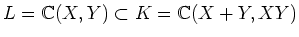
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
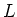
ïŋ―ïŋ―
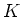
ïŋ―ïŋ―Îģïŋ―ïŋ―įžĄïŋ―ïŋ―
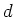
ïŋ―ïŋ―ïŋ―ČĪáĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĘĪïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
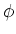
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ïŋ―
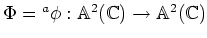
ïŋ―ïŋ―ÍĪïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
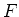
ïŋ―ĮĄïŋ―
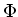
ïŋ―ïŋ―
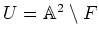
ïŋ―ØĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
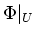
ïŋ―ïŋ―
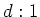
ïŋ―ČĪĘĪïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―ÎĪïŋ―ïŋ―Äļïŋ―ïŋ―ÄĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
2001-10-31
![]()