


Next: About this document ...
��������� II ���� No.3
�����Υơ���:

�������դ����褦�ˡ���Ĥ��Τδ֤ν�Ʊ����ɬ��ñ�ͤǤ��롣
�������äơ��Τδ֤ν�Ʊ����Ĵ�٤�����ϡ�
�Τδ֤Ρִޤࡢ�ޤޤ��δط��ס���ʬ�Τȳ����Τδط�)
��Ĵ�٤뤳�Ȥ˵��夵��롣
���Ԥ�����Ω�Ļ���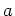 ��
�� 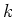 �����Ū�Ǥ���ȸ�������Ԥ�����Ω�Ļ���
�����Ū�Ǥ���ȸ�������Ԥ�����Ω�Ļ���
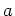 ��
�� 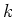 ��Ķ��Ū�Ǥ���ȸ����롣
��Ķ��Ū�Ǥ���ȸ����롣
�� (Ķ�۸��ˤ��ñ�������)
- 1.
-
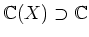
- 2.
-
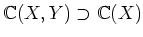
�ʲ����� 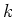 ���Ф��ơ����Ū����ȸ����Ȥ���
���Ф��ơ����Ū����ȸ����Ȥ��� 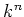 �Τ��Ȥ�
�Τ��Ȥ�
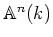 �Ƚ�
�Ƚ� 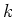 ���
��� 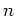 -�������ե�����֤�
��֤��Ȥˤ��롣
-�������ե�����֤�
��֤��Ȥˤ��롣
��� 3.1
���̤���
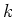
������Ū����
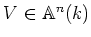
������Ǥ���Ȥ�
(��������II�Ǵ��ˤ�ä��褦��
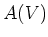
������Ǥ���Ȳ��ꤹ��Τ�Ʊ���Ǥ���)��
A(V) ���
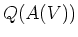
�Τ��Ȥ�
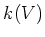
�Ƚ�
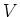
�� (
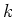
���)�ؿ��ΤȸƤ֡�
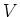 �δؿ��Τ����Ū�ʸ��ˤ��ñ����ϼ��Τ褦�ʶ��ˤʤäƤ��롣
�δؿ��Τ����Ū�ʸ��ˤ��ñ����ϼ��Τ褦�ʶ��ˤʤäƤ��롣
���� 3.1
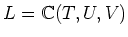
����ʬ��
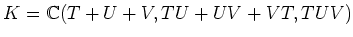
��Ȥ�ȡ�
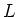
�θ�
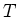
��
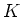
�����Ū�Ǥ��뤳�Ȥ�
��������
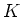
���1�ѿ�¿�༰
![$f\in K[X]$](img42.png)
�����Ū��Ϳ���뤳�ȤǼ����ʤ�����
���� 3.2
���
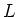
��
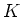
��ñ�����Ǥ��뤳�Ȥ��ʤ�����(��������Ǥ��롣)
2001-10-26
![]()
![]() ���Ф��ơ����Ū����ȸ����Ȥ���
���Ф��ơ����Ū����ȸ����Ȥ��� ![]() �Τ��Ȥ�
�Τ��Ȥ�
![]() �Ƚ�
�Ƚ� ![]() ���
��� ![]() -�������ե�����֤�
��֤��Ȥˤ��롣
-�������ե�����֤�
��֤��Ȥˤ��롣
![]() �δؿ��Τ����Ū�ʸ��ˤ��ñ����ϼ��Τ褦�ʶ��ˤʤäƤ��롣
�δؿ��Τ����Ū�ʸ��ˤ��ñ����ϼ��Τ褦�ʶ��ˤʤäƤ��롣