


Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― II 12 ïŋ―Îēïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 12.1
![$A=\mbox{${\Bbb R}$ }[X,Y,Z]$](img1.png)
ïŋ―ïŋ―ïŋ―ïŋ―
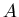
ïŋ―ØĪÎīÄ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
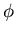
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
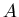
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
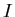
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
- 1.
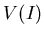 ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- 2.
-
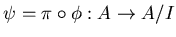 ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
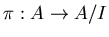 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(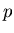 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$[p]$](img11.png) ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 3.
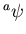 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―)
(1)
ïŋ―ïŋ―ïŋ―ηïŋ―ïŋ―Ïąïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ÃĪÆĄïŋ―ïŋ―ßĪĮĪÏĪĘĪïŋ―ïŋ―ïŋ―
(2)
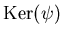 ïŋ―ïŋ―
ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ÏĪïŋ―ïŋ―ïŋ―ηŨŧïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĪŽïŋ―ïŋ―
ïŋ―ÞĪïŋ―
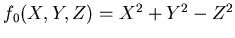 ïŋ―ïŋ―
ïŋ―ïŋ―
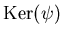 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―Į§ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―Į§ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĪïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĄïŋ―
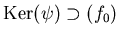 .
.
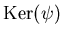 ïŋ―ïŋ―
ïŋ―ïŋ― 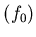 ïŋ―ČĪïŋ―ïŋ―šÝĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
ïŋ―ČĪïŋ―ïŋ―šÝĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪÏĄïŋ―
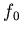 ïŋ―ËĪïŋ―ïŋ―ïŋ―ęŧŧïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―čĪĪïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËĪïŋ―ïŋ―ïŋ―ęŧŧïŋ―ïŋ―ïŋ―ïŋ―ŅĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―čĪĪïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―
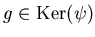 ïŋ―ïŋ―ĮĪïŋ―ÕĪËĪČĪïŋ―ČĄïŋ―
ïŋ―ïŋ―ĮĪïŋ―ÕĪËĪČĪïŋ―ČĄïŋ―
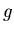 ïŋ―ïŋ―
ïŋ―ïŋ― 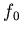 ïŋ―ïŋ―(ïŋ―Ņŋïŋ―
ïŋ―ïŋ―(ïŋ―Ņŋïŋ― 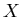 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ęĄĒ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ïŋ―)ïŋ―ïŋ―ëĪģïŋ―ČĪËĪïŋ―ęĄĒ
![$q,r\in \mbox{${\Bbb R}$ }[X,Y,Z] $](img24.png) ïŋ―ĮĄïŋ―
ïŋ―ĮĄïŋ―
ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 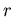 ïŋ―ïŋ―
ïŋ―ïŋ― 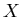 ïŋ―ËīØĪïŋ―ïŋ―랥ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―랥ïŋ―ïŋ―ïŋ―ïŋ― 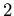 ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ČĪĘĪïŋ―ïŋ―ÎĪïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
ïŋ―Ęēïŋ―ïŋ―ïŋ―ïŋ―ČĪĘĪïŋ―ïŋ―ÎĪïŋ―Âļïŋ―ßĪïŋ―ïŋ―ëĄĢ
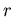 ïŋ―ïŋ―
ïŋ―ïŋ― 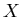 ïŋ―ËīØĪïŋ―ïŋ―ïŋ―
ïŋ―ËīØĪïŋ―ïŋ―ïŋ― 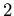 ïŋ―ïŋ―ïŋ―Ęēïŋ―ïŋ―ĘĪÎĪïŋ―ïŋ―ïŋ―ïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Ęēïŋ―ïŋ―ĘĪÎĪïŋ―ïŋ―ïŋ―ïŋ―éĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ë―ņĪĪĪÆĪßĪïŋ―ÐĄïŋ―
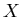 ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ÆĄïŋ―Âŋïŋ―āž°ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ηïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÜĪïŋ―ïŋ―ÆĄïŋ―Âŋïŋ―āž°ïŋ―ČĪïŋ―ïŋ―ïŋ― 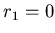 ïŋ―ïŋ― Æąïŋ―ÍĪËĪïŋ―ïŋ―ÆĄïŋ―Âŋïŋ―āž°ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ― Æąïŋ―ÍĪËĪïŋ―ïŋ―ÆĄïŋ―Âŋïŋ―āž°ïŋ―ČĪïŋ―ïŋ―ïŋ― 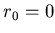 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 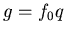 .
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―
.
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―
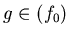 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪąïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―ïĪąïŋ―ïŋ―ïŋ―ïŋ―
(3)
ïŋ―Öĩïŋ―ïŋ―Įēïŋ―ïŋ―ŲĪïŋ―ïŋ―ÃĪïŋ―ïŋ―čĪĶïŋ―ËĪïŋ―ïŋ―ïŋ―Ïąßŋïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ― 12.2
![$B=\mbox{${\Bbb R}$ }[X,Y]$](img35.png)
ïŋ―ïŋ―ïŋ―ïŋ―
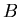
ïŋ―ØĪÎīÄ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
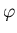
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
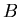
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
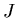
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
- 1.
- ïŋ―ïŋ―ïŋ―ïŋ―10.1 ïŋ―ËĪĘĪïŋ―ÃĪïŋ―
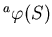 ïŋ―ōĨ°Ĩïŋ―ÕĪË―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōĨ°Ĩïŋ―ÕĪË―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 2.
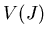 ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- 3.
-
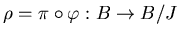 ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
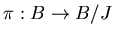 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(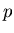 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$[p]$](img11.png) ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 4.
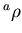 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
(ïŋ―ïŋ―ïŋ―ïŋ―)
(1)
ïŋ―ïŋ―ÎŽïŋ―ïŋ―ïŋ―ëĪŽïŋ―ïŋ―ïŋ―ÖģĘŧŌĄŨĪïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ÎĪïŋ―ÎĪËĪĘĪïŋ―ĘĪïŋ―ïŋ―ïŋ―
ïŋ―Ö°ãĪĪïŋ―ĘĪÎĪËĩïŋ―ïŋ―ÅĪïŋ―ïŋ―ïŋ―ïŋ―ßĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
Äūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ðĮ°ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ÎĪĮīïŋ―Ãąïŋ―ĘĪÏĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
(2)
ïŋ―ïŋ―ïŋ―ïŋ―ÏĪäĪĩïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘŠïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
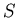 ïŋ―ïŋ―(2)ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―Ë―ņĪđïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ĘĨïŋ―ïŋ―ïŋ―ÕĪËĪĘĪëĄĢ
ïŋ―ïŋ―(2)ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―Ë―ņĪđïŋ―ïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ĘĨïŋ―ïŋ―ïŋ―ÕĪËĪĘĪëĄĢ
(3)
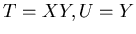 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ― 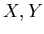 ïŋ―ÎīØ·ïŋ―ïŋ―ïŋ―
ïŋ―ÎīØ·ïŋ―ïŋ―ïŋ― 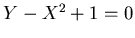 ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 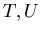 ïŋ―ÎīØ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―
ïŋ―ÎīØ·ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ― 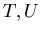 ïŋ―ïŋ―
ïŋ―ïŋ― 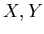 ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―Ï·ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÖĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÐĪčĪĪïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―Îūïŋ―ïŋ―Ï·ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ― 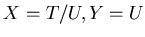 ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĩÕĪËēōĪąĪëĪŦïŋ―ïŋ―ÚĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―Ę·Ũŧïŋ―ïŋ―ōĪ·Īïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―12.1ïŋ―ïŋ―(2)ïŋ―Îēïŋ―ïŋ―ïŋ―Į―ŌĪŲĪïŋ―ïŋ―čĪĶïŋ―ĘĨïŋ―ïŋ―ïŋ―ïŋ―ÃĨïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ŲĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĩÕĪËēōĪąĪëĪŦïŋ―ïŋ―ÚĪĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―Ę·Ũŧïŋ―ïŋ―ōĪ·Īïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―12.1ïŋ―ïŋ―(2)ïŋ―Îēïŋ―ïŋ―ïŋ―Į―ŌĪŲĪïŋ―ïŋ―čĪĶïŋ―ĘĨïŋ―ïŋ―ïŋ―ïŋ―ÃĨïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ïŋ―ŲĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
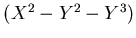
(4)
ïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪïŋ―Öĩïŋ―ïŋ―Į―ņĪĪĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆūÜĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ïūïŋ―ÎŽïŋ―ïŋ―ïŋ―ëĄĢ (1)ïŋ―ïŋ―(3)ïŋ―ČĪïŋ―Æąïŋ―ïŋ―ïŋ―Ë―ņĪŊĪČĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ËĪĘĪëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪïŋ―ïŋ―ïŋ―ŲĪïŋ―Čēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÃĪÆĪïŋ―ïŋ―ëĪŦĘŽïŋ―ïŋ―ïŋ―ïŋ―äĪđïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÕĪōĨđĨïŋ―ïŋ―ïŋ―Ë―ņĪĪĪÆĪïŋ―ïŋ―ïŋ―ïŋ―ÆĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ÕĪïŋ―ŌĪÃĪïŋ―ïŋ―ïŋ―ïŋ―ÖĪïŋ―(ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪÍĪęĪŽïŋ―ÃĪïŋ―ïŋ―)ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―įĪĶïŋ―ÉĪïŋ―ïŋ―ÎĪčĪĶïŋ―Ę·ïŋ―ïŋ―ËĪĘĪëĄĢïŋ―
Yoshifumi Tsuchimoto
2001-07-24
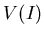 ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
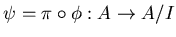 ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
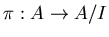 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(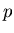 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$[p]$](img11.png) ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
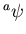 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
![\includegraphics[scale=0.5]{tube.ps}](img13.png)
![\includegraphics[scale=0.5]{cone.ps}](img34.png)
![\includegraphics[scale=0.5]{parabora.ps}](img48.png)
![\includegraphics[scale=0.5]{singular.ps}](img55.png)