


Next: About this document ...
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― II ïŋ―ïŋ―ïŋ―ïŋ― No.12
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĨÆĄïŋ―ïŋ―ïŋ―:
ïŋ―ïŋ―ïŋ― 12.1
ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―
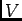
ïŋ―Κïŋ―Éļïŋ―ïŋ―
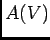
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
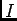
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ėĪŋïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÏĪïŋ―ÏĪïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ― (
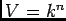
ïŋ―Îŧïŋ―ïŋ―ïŋ―Æąïŋ―ÍĪËĄïŋ―)
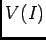
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 12.1
ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―
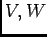
ïŋ―ÎīÖĪïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ïŋ―
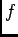
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
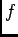
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Øŋïŋ―ïŋ―ÄĪÎ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―(ïŋ―Ö°ïŋ―ïŋ―ïŋ―ïŋ―áĪ·ïŋ―ïŋ―)
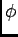
ïŋ―ÎģËĪïŋ―
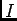
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĐïŋ―ÄĄïŋ―
- 1.
-
- 2.
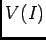 ïŋ―ïŋ―
ïŋ―ïŋ―
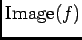 ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆīÞĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ÆīÞĪïŋ― 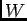 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Įūïŋ―ïŋ―ÎĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
(Zariski ïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ÕĪĮĪïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Įūïŋ―ïŋ―ÎĪïŋ―ÎĪĮĪïŋ―ïŋ―ëĄĢ
(Zariski ïŋ―ïŋ―ïŋ―ïŋ―Îļïŋ―ïŋ―ÕĪĮĪïŋ―ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ïŋ―ïŋ― 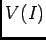 ïŋ―ïŋ―
ïŋ―ïŋ―
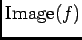 ïŋ―ïŋ―(Zariskiïŋ―ïŋ―ïŋ―ïŋ―ËīØĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―Čļïŋ―ïŋ―ÃĪÆĪâĪŠïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―(Zariskiïŋ―ïŋ―ïŋ―ïŋ―ËīØĪïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―Čļïŋ―ïŋ―ÃĪÆĪâĪŠïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪĮĪïŋ―ïŋ―ëĄĢ)
ïŋ―ïŋ―ïŋ―ïŋ―ÞĪĮĪÎĪČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ãąïŋ―ïŋ―É―ïŋ―ËĪÞĪČĪïŋ―ïŋ―ČĄïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―Ęķïŋ―ïŋ―ËĪĘĪëĄĢ
| ïŋ―ïŋ―ïŋ―ïŋ― |
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― |
| ïŋ―ÖĨïŋ―ÎĄŨĪïŋ―ïŋ―Ðąïŋ― |
Âŋïŋ―āž°ïŋ―ïŋ―
![$k[X_1,X_2,\dots,X_n]$](img14.png) |
nïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― 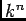 ïŋ―Κïŋ―Éļïŋ―ïŋ―
ïŋ―Κïŋ―Éļïŋ―ïŋ― |
ïŋ―ïŋ― 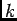 ïŋ―ïŋ―ÞĪïŋ―ïŋ―
ïŋ―ïŋ―ÞĪïŋ―ïŋ― 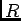 |
ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ― 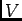 ïŋ―Κïŋ―Éļïŋ―ïŋ― A(V)
ïŋ―Κïŋ―Éļïŋ―ïŋ― A(V) |
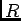 ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ― 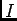 |
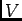 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―(Zariski ïŋ―Ä―ïŋ―ïŋ―ïŋ―)
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―(Zariski ïŋ―Ä―ïŋ―ïŋ―ïŋ―) 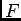 ïŋ―ïŋ―
ïŋ―ïŋ― |
| |
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪĘĪïŋ―Øŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ― |
ïŋ―ïŋ―Íūïŋ―ïŋ― 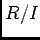 |
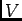 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ― 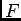 ïŋ―Κïŋ―Éļïŋ―ïŋ― A(F)
ïŋ―Κïŋ―Éļïŋ―ïŋ― A(F) |
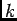 -ïŋ―ïŋ―Æąïŋ―ïŋ― -ïŋ―ïŋ―Æąïŋ―ïŋ―
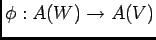 |
ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ÎīÖĪïŋ―Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ïŋ―
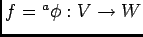 |
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―Îģïŋ―
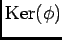 |
Âŋïŋ―āž°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― Zariski ïŋ―ïŋ―ïŋ―ïŋ―
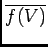 |
| ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŨĪïŋ―ïŋ―Ðąïŋ― |
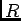 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ęķïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― |
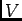 ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÎļïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Â―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÄĪÎļïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Â―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ïŋ― |
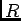 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŌĪïŋ―ïŋ―ïŋ―ïŋ― |
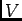 ïŋ―Ïēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―Ïēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ïŋ―ïŋ―ïŋ― |
ïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ÏĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ÞĪïŋ―ïŋ―ĘĪïŋ―ÎĪĮĄïŋ―ïŋ―ïŋ―ĖĐïŋ―ËĪÏĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ŲĪÎūïŋ―ïĪŽïŋ―ĘĪïŋ―ïŋ―Čšïŋ―ïŋ―ïŋ―ïŋ―Îđïŋ―ïŋ―ÜĪïŋ―
ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ÃĪïŋ―ïŋ―ęĄĒïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―âĪĒïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎūÜšŲĪËĪÄĪïŋ―ïŋ―ÆĪÏĪïŋ―ïŋ―ėĪūïŋ―ïŋ―Îēïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ōŧēūČĪïŋ―ïŋ―ėĪŋïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ËĪÏĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÅŠïŋ―ĘĨïŋ―ïŋ―ᥞïŋ―ïŋ―ïŋ―ōĪĶĪÞĪïŋ―ïŋ―ČĪÃĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Ä°ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪĘūïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÄĪïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―čĪĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 12.1
![$A=\mbox{${\Bbb R}$ }[X,Y,Z]$](img24.png)
ïŋ―ïŋ―ïŋ―ïŋ―
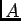
ïŋ―ØĪÎīÄ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
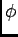
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
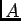
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
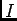
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
- 1.
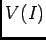 ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- 2.
-
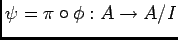 ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
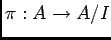 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(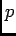 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$[p]$](img31.png) ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 3.
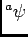 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― 12.2
![$B=\mbox{${\Bbb R}$ }[X,Y]$](img33.png)
ïŋ―ïŋ―ïŋ―ïŋ―
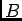
ïŋ―ØĪÎīÄ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
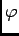
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―
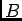
ïŋ―ÎĨïŋ―ïŋ―ĮĨïŋ―ïŋ―ïŋ―
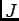
ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢïŋ―ïŋ―ïŋ―ÎĪČĪïŋ―ïŋ―ïŋ―
- 1.
- ïŋ―ïŋ―ïŋ―ïŋ―10.1 ïŋ―ËĪĘĪïŋ―ÃĪïŋ―
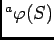 ïŋ―ōĨ°Ĩïŋ―ÕĪË―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ōĨ°Ĩïŋ―ÕĪË―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 2.
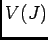 ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎĨïŋ―ïŋ―ïŋ―ÕĪÎģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
- 3.
-
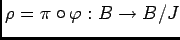 ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ÎģËĪïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
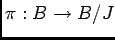 ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(
ïŋ―Ïžïŋ―ïŋ―ïŋ―ïŋ―ʞ͹ïŋ―
(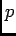 ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ
ïŋ―ïŋ―ïŋ―ÐĪïŋ―ïŋ―ÆĪïŋ―ïŋ―ÎĨïŋ―ïŋ―éĨđ ![$[p]$](img31.png) ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―Ðąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―)ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
- 4.
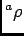 ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Îģïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ņĪĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―1, 2 ïŋ―ČĪïŋ―Ëĩïŋ―ïŋ―ïŋ―ïŋ―ÎĪÛĪïŋ―ïŋ―ïŋ―Ũŧïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ÞĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĪÎĪïŋ―ïŋ―ïŋ―ïŋ―ÕĄïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ÕĪČĪčĪŊïŋ―ïŋ―ïŋ―ïŋ―ŲĪÆĪßĪïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ËĄïŋ―MuPAD ïŋ―ĘĪÉĪĮžÂšÝĪËĨïŋ―ïŋ―ïŋ―ÕĪōļŦĪÆĪßĪïŋ―ČĪïŋ―ÃĪČĪčĪĪïŋ―ïŋ―
MuPAD ïŋ―Ïđïŋ―ïŋ―ïŋ―ïŋ―įĪŦïŋ―ïŋ―ĘĪïŋ―
http://www.math.kochi-u.ac.jp/docky/kogi/
ïŋ―ĮĨïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪĮĪïŋ―ïŋ―ëĄĢ



Next: About this document ...
2001-07-24
![]()