


Next: About this document ...
����� II ���� No.2
�����Υơ���:
����ץ��ȤˤϽʤ��ä��������ιֵ��ǤϤȤ����Ǥ�ʤ��¤�ִġפȤ�����
ñ�̸�����IJĴ��ĤΤ��Ȥ��̣���롣
(�ʤ���Ϸ�̿��ʤ��顢����Ρ����1.1�פϤ����Ȥ�������ǤϤʤ���
���Τ�����������C �ޤ��������I�ιֵ��dzؤ�Ǥ���Ϥ��Ǥ��롣)
(����)
���̤ˡ��� 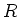 �θ�
�θ�
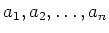 ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���
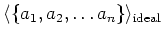 �Τ��Ȥ�ñ��
�Τ��Ȥ�ñ��
�ȴݳ�̤�Ȥäƽ��Ȥ�¿�������̤˿��ؤǤϴݳ�̤����̤ʰ�̣��⤿���뤳�Ȥ�
���ޤ�ʤ��������Ρ�...����������륤�ǥ���פ��㳰�Ǥ��롣
���ؤǤϤ褯�Ѥ����뤷���ڤǤ⤢��Τǡ��ֵܹ��Ǥ⤳�ε�����Ѥ��뤳�Ȥ�
���뤬�����𤷤ʤ��褦�˽�ʬ���դ��뤳�ȡ�
���� 2.1
��
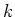
����������
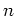
��Ϳ�����Ƥ���Ȥ��롣
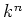
����ʬ����
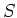
�ˤ������ơ�
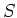
���
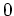
�ˤʤ�¿�༰������
��
![$k[X_1,X_2,\dots,X_n]$](img17.png)
�Υ��ǥ���Ǥ��롣
���� 2.2
��
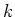
����������
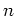
��Ϳ�����Ƥ���Ȥ��롣
![$R=k[X_1,X_2,\dots,X_n]$](img18.png)
����ʬ����
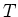
���Ф��ơ�
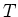
����������
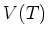
��
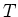
���������줿
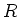
�Υ��ǥ���
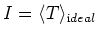
����������
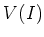
�Ȱ��פ��롣
�� 2.1
��
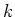
����������
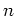
��Ϳ�����Ƥ���Ȥ��롣
![$R=k[X_1,X_2,\dots,X_n]$](img18.png)
����ʬ����
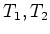
�����äơ��⤷
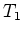
���������줿
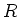
�Υ��ǥ����
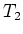
���������줿
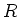
�Υ��ǥ��뤬
���פ��롢���ʤ��
������Ω�Ĥʤ�С�
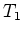
�����������
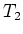
�����������
���פ��롣���ʤ��
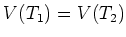
�Ǥ��롣
�����ͳ���顢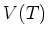 ��
�� 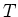 �����ǥ���ΤȤ��Τߤ�ͤ���Ф��夦�֤�Ǥ��롣
���̤ˡ�
�����ǥ���ΤȤ��Τߤ�ͤ���Ф��夦�֤�Ǥ��롣
���̤ˡ�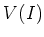 �η��ν�������Ū����ȸƤ֡�
�η��ν�������Ū����ȸƤ֡�
(����)
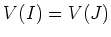 ������Ȥ��ä�
������Ȥ��ä� 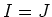 �Ȥϸ¤�ʤ���
�Ȥϸ¤�ʤ���
���� 2.3
��
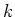
����������
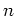
�ᡢ
![$R=k[X_1,\dots X_n]$](img29.png)
�Ȥ�����
���ΤȤ���
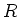
�Υ��ǥ��������������Ф��Ƽ��ν���������Ω�ġ�
- 1.
-
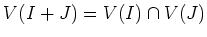
- 2.
- ��äȰ��̤�
- 3.
-
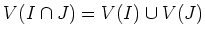
- 4.
-
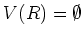
- 5.
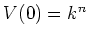
�� 2.2
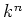
�ϡ����Ū��������Τ��Ľ���Ȥ��ơ�������֤�ʤ���
���ΰ���Τ��Ȥ� Zariski ����ȸƤ֡�
Zariski �������������ؤǴ���Ū������̤�����
���ΰ����(�褯�Ȥ������Τʤ��Ǥ�������)Hausdorff ���֤ǤϤʤ���
���� 2.1
- 1.
-
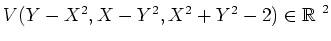 ������ʤ�����
������ʤ�����
- 2.
- ���ǥ��������
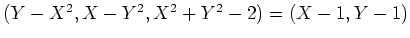 ��������ʤ�����
��������ʤ�����
(����)
1. �� 2. ��ͤ����ǥҥ�ȤˤϤʤ뤬��2.�ξ����� 1. �Ȥ��̤�
�դ���ɬ�פ����롣
Yoshifumi Tsuchimoto
2001-05-01
![]()
![]() �θ�
�θ�
![]() ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���
![]() �Τ��Ȥ�ñ��
�Τ��Ȥ�ñ��
![]() ��
�� ![]() �����ǥ���ΤȤ��Τߤ�ͤ���Ф��夦�֤�Ǥ��롣
���̤ˡ�
�����ǥ���ΤȤ��Τߤ�ͤ���Ф��夦�֤�Ǥ��롣
���̤ˡ�![]() �η��ν�������Ū����ȸƤ֡�
�η��ν�������Ū����ȸƤ֡�
![]() ������Ȥ��ä�
������Ȥ��ä� ![]() �Ȥϸ¤�ʤ���
�Ȥϸ¤�ʤ���