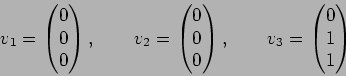![]()
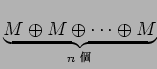 魹スリ、魹ス
魹スリ、魹ス
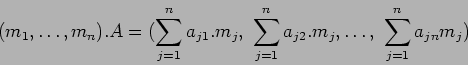
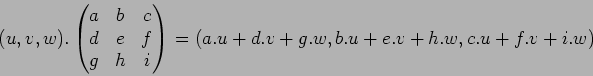
(魹ス魹ス魹ス魹ス):
![]() 魹スホ、魹ス魹スネ、魹スホャ魹ス魹ス魹ス魹ス
魹スホ、魹ス魹スネ、魹スホャ魹ス魹ス魹ス魹ス![]() 魹スネ、魹ス魹ス魹ス魹ス魹ス
魹スネ、魹ス魹ス魹ス魹ス魹ス
![]() 魹ス魹ス
魹ス魹ス ![]() 魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス ![]() 魹ズ、魹スニー魹ス魹ス魹ス魹ステ、ニ、魹ス魹ス魹ス顬ア魹スヌ、魹ス魹ス槶ャ魹ス魹ス
魹ス魹ス魹スホ、隍ヲ魹ス魹スホャ魹ス魹ス魹ス魹ス魹スマス魹ス魹ス魹ス魹スマソ魹ス魹ス魹ス魹スハウリアムク琨シ魹ス゚・ハ。魹ス魹ス魹スヌ、魹ス魹スハ、魹ス魹ス゚、ハ、マ、魹ス魹スヌ、魹ス魹ス槩」
魹スハイ魹ス魹スホ、魹ス魹ス琦セ魹ス魹スホシ魹ス魹スヌ、ノ、魹ス魹スムソ魹ス魹ス魹スニー魹ス魹ス魹ス魹ス槶ォ魹スヒ、マ、ネ、魹ス魹ス魹ス魹ス魹ス魹スユ、魹ス魹スラ、魹ス魹ス槩」
魹ス魹ス魹ス魹スヌ、魹スハャ魹ス魹ス魹ス魹スヒ、魹ス魹ス魹ス魹スネサラ、魹ス魹スヘ、魹ス
魹ズ、魹スニー魹ス魹ス魹ス魹ステ、ニ、魹ス魹ス魹ス顬ア魹スヌ、魹ス魹ス槶ャ魹ス魹ス
魹ス魹ス魹スホ、隍ヲ魹ス魹スホャ魹ス魹ス魹ス魹ス魹スマス魹ス魹ス魹ス魹スマソ魹ス魹ス魹ス魹スハウリアムク琨シ魹ス゚・ハ。魹ス魹ス魹スヌ、魹ス魹スハ、魹ス魹ス゚、ハ、マ、魹ス魹スヌ、魹ス魹ス槩」
魹スハイ魹ス魹スホ、魹ス魹ス琦セ魹ス魹スホシ魹ス魹スヌ、ノ、魹ス魹スムソ魹ス魹ス魹スニー魹ス魹ス魹ス魹ス槶ォ魹スヒ、マ、ネ、魹ス魹ス魹ス魹ス魹ス魹スユ、魹ス魹スラ、魹ス魹ス槩」
魹ス魹ス魹ス魹スヌ、魹スハャ魹ス魹ス魹ス魹スヒ、魹ス魹ス魹ス魹スネサラ、魹ス魹スヘ、魹ス
![]() 魹ス魹ス
魹ス魹ス ![]() 魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹スモ、魹ス魹スニ、魹ス隍、魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹スヒサ魹ス魹スヒ、ハ、槶ウ魹スネ、魹ス
魹スミク遉サ魹スヘ、ミ、ハ、魹スハ、魹ス魹ス魹ス
魹スツ、ホオ魹ス魹ス魹ス
魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹スモ、魹ス魹スニ、魹ス隍、魹ス魹ス魹ス魹ス魹ス魹ス魹スハ、魹ス魹スヒサ魹ス魹スヒ、ハ、槶ウ魹スネ、魹ス
魹スミク遉サ魹スヘ、ミ、ハ、魹スハ、魹ス魹ス魹ス
魹スツ、ホオ魹ス魹ス魹ス ![]() 魹ス魹ス魹ス魹ス魹ズ、魹ス魹スネ、魹ス魹ス槶ウ魹スネ。魹ス
魹スネ、魹ス魹スヒ、ノ、魹スナコ魹ス魹ス魹ス魹ス魹スユ、魹ス魹ス魹ス魹スツ、魹スネ、テ、ニ、魹ス魹ス槶ォ魹ス魹ス魹ス魹ス魹ス魹スヌ。魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、マ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヨ、ホ・ン・魹ス魹ス魹スネ、ヌ、魹ス魹ス槩」
(魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハウ魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、ハ、魹ス魹ス魹ス魹ス魹ス)
(魹ス魹ス魹ス魹ス):
魹ス魹ス魹ス魹ス魹ズ、魹ス魹スネ、魹ス魹ス槶ウ魹スネ。魹ス
魹スネ、魹ス魹スヒ、ノ、魹スナコ魹ス魹ス魹ス魹ス魹スユ、魹ス魹ス魹ス魹スツ、魹スネ、テ、ニ、魹ス魹ス槶ォ魹ス魹ス魹ス魹ス魹ス魹スヌ。魹ス
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ、マ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヨ、ホ・ン・魹ス魹ス魹スネ、ヌ、魹ス魹ス槩」
(魹スネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スハウ魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、ハ、魹ス魹ス魹ス魹ス魹ス)
(魹ス魹ス魹ス魹ス):
![]() 魹スネ、魹ス魹ス魹スネ。魹ス
魹スネ、魹ス魹ス魹スネ。魹ス

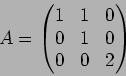
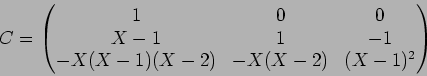
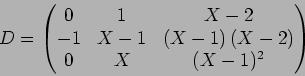
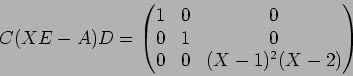
魹ス魹ス魹スホセ魹ス魹ス魹ス魹スホイ魹ス魹スヌ。魹ス
魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹ス魹ステ、ネ、魹ス荀ウ魹ス魹ス魹ス魹ス魹ステ、魹ス魹ス魹ス魹ス魹ス魹スホ、魹スハ、魹ス魹ス魹ス
魹スニ・晬ス・魹ス魹スム、魹ス魹ス庹ア、魹ス魹ス魹ス魹ス癸「![]() 魹ス魹ス魹ス魹スト、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス顬サ魹スニ、魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス鬢キ魹ス魹ス魹ス魹ス
魹スネ、魹ス魹スヒ。魹ス
魹ス魹ス魹ス魹スト、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス顬サ魹スニ、魹ス魹ス魹スネ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹ス魹ス鬢キ魹ス魹ス魹ス魹ス
魹スネ、魹ス魹スヒ。魹ス
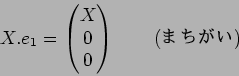
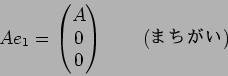
(魹ス魹ス魹ス魹ス):
1.
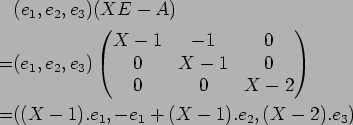
魹ス魹ス魹ス魹ス魹ス魹ス魹ス鬢ャ魹ス魹ス魹ス魹スヌ。魹ス
魹ス魹ス魹ス魹スヒ、魹ス魹ス魹ス隍ヲ魹ス魹ス ![]() 魹ス魹ス
魹ス魹ス
![]() 魹スリ、ホコ魹ス魹スム、魹ス
魹スリ、ホコ魹ス魹スム、魹ス ![]() 魹スヒ、魹ス槶ォ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス
魹スヒ、魹ス槶ォ魹ス魹ス魹ス魹ス魹スヌ、魹ス魹ス槩」
魹ス魹ス魹ス魹ス魹ス魹ス魹ステ、ニ。魹ス
2. 魹ス魹ス魹ス魹ス魹ステア魹ス魹スラサ魹ス魹スヌ、魹ス魹ス槩」魹ス魹ス魹スヨサ魹ス魹スヨ、魹スネ、魹スネ、魹ス魹ス魹ス魹スヌ、魹ス魹ス槶ャ魹ス魹ス
魹ス魹ス魹ス魹ス魹スホ、ネ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホィ魹ス魹ス魹ス筅ォ魹ステ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス
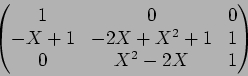
魹スハ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スホイ魹ス魹ス魹ス魹ス魹ス魹ス魹スヌ。魹ス![]() 魹ス魹ス魹スムソ魹ス魹スヌ、マ、ハ、魹ス魹ス魹ス
魹ス魹ス魹スムソ魹ス魹スヌ、マ、ハ、魹ス魹ス魹ス
![]() 魹スホク魹ス魹ス魹ス魹スホ、魹ス魹スネ、魹ス
魹ス魹ス魹スト、魹ス魹ステ、ニ、魹ス魹ス魹スハェ魹ス魹ス魹ス魹ス魹ステ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹スホ、゙、゙、ヌ、マエヨー网、魹スヌ、魹ス魹ス槩」
(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ。魹ス筅「魹ス槶ャ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹スホ、隍ヲ魹スハ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹スネ、魹ス魹スロ、ノ、魹ス
魹ス魹スホ、ヌ、マ、ハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スホイ魹ス魹ス魹ス魹ス魹ス㖨、、魹ス魹スヘ、魹ス魹ス魹ス魹スホ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹ス魹スネ、魹ス魹スニ、魹ス魹ス魹スネ、マケヘ、魹ス魹スヒ、魹ス魹ス魹ス魹ス魹ス)
魹スホク魹ス魹ス魹ス魹スホ、魹ス魹スネ、魹ス
魹ス魹ス魹スト、魹ス魹ステ、ニ、魹ス魹ス魹スハェ魹ス魹ス魹ス魹ス魹ステ、魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹スホ、゙、゙、ヌ、マエヨー网、魹スヌ、魹ス魹ス槩」
(魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ。魹ス筅「魹ス槶ャ魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマ、魹ス魹スホ、隍ヲ魹スハ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹スネ、魹ス魹スロ、ノ、魹ス
魹ス魹スホ、ヌ、マ、ハ、魹ス魹ス魹ス魹ス魹ス
魹ス魹ス魹スホイ魹ス魹ス魹ス魹ス魹ス㖨、、魹ス魹スヘ、魹ス魹ス魹ス魹スホ・ニ・魹ス魹スヒ・テ・魹ス魹ス魹ス魹スネ、魹ス魹スニ、魹ス魹ス魹スネ、マケヘ、魹ス魹スヒ、魹ス魹ス魹ス魹ス魹ス)
3.
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スマエ魹ステア魹ス魹ス魹ス魹ス魹ス魹ス魹スホ、ヌス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹スヒ、魹ス魹ス魹ス魹ステ、魹ス魹スホ、魹ス魹ス魹ス魹スホ、魹スハ、魹ス魹ス魹ス
![]() 魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス鬘「
魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス魹ス鬘「
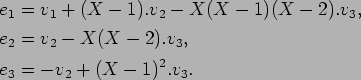
4.
魹ス魹ス魹ス魹ス魹ス 2. 魹スホキ魹スフ、魹スネ、魹ス魹ス魹ス
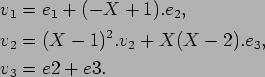
魹スヌ、魹ス魹ス遙「1. 魹ス魹スニア魹スヘ、ヒキラサ魹ス魹ス魹ス魹ス魹スミ。魹ス