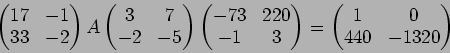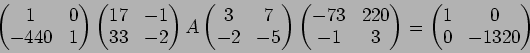Next: About this document ...
пњљпњљпњљпњљпњљпњљпњљпњљпњљ I пњљпњљпњљпњљ No.10
пњљпњљпњљпњљпњљќ•∆°пњљпњљпњљ:
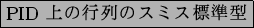
(пњљпњљЋ°)
пњљƒіпњљпњљпњљ  пњљЋ§ƒ§пњљпњљ∆°пњљпњљпњљпњљќ§и§¶пњљ µпњљпњљпњљпњљпњљ—§пњљпњљл°£
пњљЋ§ƒ§пњљпњљ∆°пњљпњљпњљпњљќ§и§¶пњљ µпњљпњљпњљпњљпњљ—§пњљпњљл°£
пњљпњљпњљпњљ 10.1
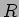
пњљпњљPIDпњљ«°пњљ
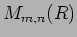
пњљќЄпњљ
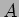
пњљпњљЌњпњљпњљпњљпњљпњљ∆§пњљпњљпњљ»§пњљпњљл°£
пњљпњљпњљќ§»§пњљпњљпњљ
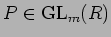
пњљпњљ
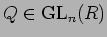
пњљ»§т§¶§ё§пњљЌњпњљпњљпњљпњљ–°пњљ
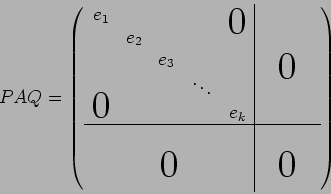
PAQ пњљѕЉпњљпњљќ§и§¶пњљ ЈпњљпњљЋ§«§пњљпњљл°£
(
пњљпњљпњљпњљпњљпњљ,
 пњљпњљ
пњљпњљ 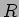 пњљќЄпњљпњљ«°пњљ
пњљќЄпњљпњљ«°пњљ
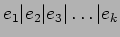 пњљпњљпњљ §к§њпњљƒ°пњљ)
пњљпњљпњљ §к§њпњљƒ°пњљ)
пњљпњљпњљпњљпњљпњљпњљпњљпњљќЊпњљпњљпњљпњљпњљпњљ№Љпњљ≈™пњљЋ§пњљ 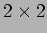 пњљпњљпњљпњљпњљпњљ√§пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљ√§пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
㧮
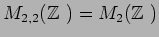 пњљќЄпњљ
пњљќЄпњљ
пњљпњљпњљпњљпњљпњљпњљпњљл°£пњљё§пњљ  пњљпњљ
пњљпњљ 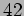 (пњљпњљ1пњљпњљ)пњљ»§«•ж°Љпњљпњљпњљпњљ√•…§ќЄяљпњљЋ°(gcd пњљпњљ6)пњљпњљ‘§пњљпњљпњљ
(пњљпњљ1пњљпњљ)пњљ»§«•ж°Љпњљпњљпњљпњљ√•…§ќЄяљпњљЋ°(gcd пњљпњљ6)пњљпњљ‘§пњљпњљпњљ
пњљ»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ(пњљпњљпњљќЉпњљпњљЋ§пњљпњљпњљпњљпњљпњљќ§ѕ∞пњљпњљћ§пњљPID 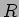 пњљ«§ѕ•пњљпњљ«•пњљпњљпњљќµпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£)
пњљпњљпњљпњљпњљ№§ќЉпњљпњљпњљпњљпњљ
пњљ«§ѕ•пњљпњљ«•пњљпњљпњљќµпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£)
пњљпњљпњљпњљпњљ№§ќЉпњљпњљпњљпњљпњљ
пњљпњљ
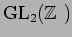 пњљќЄпњљпњљ«§пњљпњљл§≥пњљ»§пњљпњљп§Ђпњљл°£
пњљќЄпњљпњљ«§пњљпњљл§≥пњљ»§пњљпњљп§Ђпњљл°£
пњљпњљпњљў§ѕ°пњљ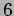 пњљпњљ
пњљпњљ  (пњљпњљ1пњљпњљ)пњљ»§пњљ∆±пњљЌ§ §пњљпњљ»§пњљ‘§пњљпњљпњљ
(пњљпњљ1пњљпњљ)пњљ»§пњљ∆±пњљЌ§ §пњљпњљ»§пњљ‘§пњљпњљпњљ
пњљпњљпњљў§ѕЇ∆§пњљ1пњљ‘§пњљ∆±пњљЌ§пњљпњљпњљпњљпњљ‘§пњљпњљпњљ
(1,1)-пњљпњљ ђпњљпњљпњљ °пњљ``пњљпњљпњљпњљпњљпњљ''пњљ §√§∆§пњљпњљпњљпњљпњљпњљ»§пњљпњљпњљпњљ’°пњљ
пњљ«ЄпњљЋ§в§¶пњљпњљпњљпњљпњљпњљпњљпњљпњљЋ§ƒ§пњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§є§л°£
пњљпњљ…°пњљ
пњљпњљпњљ÷§пњљпњљ–§и§§пњљпњљ
пњљпњљпњљпњљпњљќ§и§¶пњљ Ј„їпњљпњљпњљпњљпњљпњљƒ§«§пњљя§ё§л§≥пњљ»§т§§§пњљпњљЋ§ѕ°пњљ
пњљпњљPID пњљќ•пњљпњљ«•пњљпњљпњљпњљпњљпњљпњљпњљпњљу§ђ§пњљпњљƒ§«§пњљ…§пњљпњљпњљпњљ«§»§ё§пњљ„§»§пњљпњљпњљпњљпњљпњљ¬§пњљ
пњљпњљпњљ’§пњљпњљпњљ–§и§§пњљпњљпњљпњљпњљќїпњљпњљ¬Љпњљпњљќ§пњљпњљпњљпњљIпњљ«§пњљпњљ«§Ћљ–§∆§пњљпњљ∆§пњљпњљпњљѕ§пњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљ∆±пњљпњљпњљпњљпњљ»§т§є§пњљќ§ѕ§–§пњљпњљ–§пњљпњљпњљпњљпњљпњљќ§«°пњљ
пњљпњљпњљ»§пњљпњљ»§ќ§пњљпњљпњљпњљЌ§пњљпњљ∆§пњљпњљќїпњљпњљ¬§ќ≥пњљƒ•пњљ«§пњљпњљл°Ґ
пњљпњљпњљћ§ќ•Ќ°пњљпњљпњљпњљпњљпњљƒ§пњљпњљпњљƒІпњљ’§пњљпњљЋ§ƒ§пњљпњљ∆§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљл°£
пњљпњљпњљпњљ 10.1
- 1.
- пњљƒіпњљпњљЌ°пњљпњљпњљпњљпњљпњљпњљ
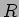 пњљќ•пњљпњљ«•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљќ•пњљпњљ«•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљ…ђпњљпњљпњљ…§пњљпњљпњљпњљ«їя§ё§л°£пњљпњљпњљ §пњљпњљпњљпњљпњљпњљпњљпњљ 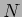 пњљпњљпњљпњљпњљ√§∆°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљпњљпњљ√§∆°пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ
пњљпњљпњљ §к§њпњљƒ°пњљ
- 2.
- пњљ’§Ћ°пњљпњљƒіпњљпњљпњљ
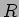 пњљпњљпњљпњљ
пњљпњљпњљпњљ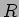 пњљќ•пњљпњљ«•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ…ђпњљпњљпњљ…§пњљпњљпњљпњљ«їя§ё§пњљпњљ
пњљ»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ∆§–°пњљ
пњљќ•пњљпњљ«•пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ…ђпњљпњљпњљ…§пњљпњљпњљпњљ«їя§ё§пњљпњљ
пњљ»§пњљпњљпњљпњљпњљпњљпњљпњљпњљпњљ∆§–°пњљ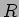 пњљѕ•Ќ°пњљпњљпњљпњљпњљпњљƒ§«§пњљпњљл°£
пњљѕ•Ќ°пњљпњљпњљпњљпњљпњљƒ§«§пњљпњљл°£
пњљпњљпњљпњљ 10.1
![$R={\Bbb C}[X]$](img31.png)
пњљ»§пњљпњљл°£
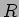
пњљпњљќєпњљпњљпњљ
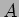
пњљт≤Љ§ќ§и§¶пњљЋЈпњљпњљпњљ»§пњљпњљпњљ
пњљпњљпњљпњљ10.1 пњљпњљ
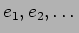
пњљЋ§пњљпњљпњљпњљпњљпњљќ§т§љ§м§Њпњљпњљпњљпњљи°£
(пњљпњљЌ≥пњљ’§пњљпњљт§≠§пњљпњљпњљ»љс§§§∆§пњљпњљпњљ–°пњљпњљ»§пњљпњљпњљ
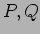
пњљпњљпњљпњљпњљ…ђпњљ„§ѕ§ §пњљпњљпњљ)
- 1.
-
- 2.
-
- 3.
-
(пњљ“•пњљпњљ:
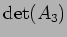 пњљѕ§пњљпњљпњљпњљй§Ђпњљпњљ)
пњљѕ§пњљпњљпњљпњљй§Ђпњљпњљ)
- 4.
-



Next: About this document ...
Yoshifumi Tsuchimoto
2000-12-04
![]()
![]() пњљЋ§ƒ§пњљпњљ∆°пњљпњљпњљпњљќ§и§¶пњљ µпњљпњљпњљпњљпњљ—§пњљпњљл°£
пњљЋ§ƒ§пњљпњљ∆°пњљпњљпњљпњљќ§и§¶пњљ µпњљпњљпњљпњљпњљ—§пњљпњљл°£
![]() пњљпњљ
пњљпњљ ![]() пњљќЄпњљпњљ«°пњљ
пњљќЄпњљпњљ«°пњљ
![]() пњљпњљпњљ §к§њпњљƒ°пњљ)
пњљпњљпњљ §к§њпњљƒ°пњљ)
![]() пњљпњљпњљпњљпњљпњљ√§пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
пњљпњљпњљпњљпњљпњљ√§пњљпњљпњљпњљпњљпњљпњљпњљпњљ«§пњљпњљл°£
![]() пњљќЄпњљ
пњљќЄпњљ