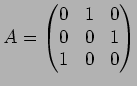 ,
,
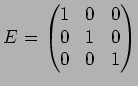 ,
,
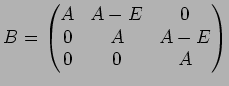 ��������������
��������������
![]() �Ȥ�����
���ΤȤ���
�Ȥ�����
���ΤȤ���
- 1.
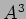 ����ʤ�����
����ʤ�����
����:
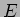 .
(�����ñ����Ǥ��뤬��
���ܥ٥��ȥ�ιԤ��� (
.
(�����ñ����Ǥ��뤬��
���ܥ٥��ȥ�ιԤ��� (
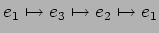 )��
���Ƥ�������㴳�ᤤ��)
)��
���Ƥ�������㴳�ᤤ��)
- 2.
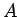 �θ�ͭ�ͤ٤Ƶ��ʤ�����
�θ�ͭ�ͤ٤Ƶ��ʤ�����
����:
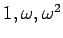 .
(������ñ���������ʤ������ 1.�η�̤��顢
.
(������ñ���������ʤ������ 1.�η�̤��顢 �θ�ͭ�ͤ�ɬ��
3�褷��
�θ�ͭ�ͤ�ɬ��
3�褷��  �ˤʤ뤳�Ȥ�狼�äƤ���Ϥ��Ǥ��롣)
�ˤʤ뤳�Ȥ�狼�äƤ���Ϥ��Ǥ��롣)
- 3.
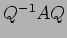 ���гѹ���Ǥ���褦����§����
���гѹ���Ǥ���褦����§����  ���ĵ��ʤ�����
���ĵ��ʤ�����
����:
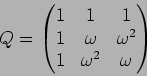
(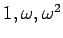 ���Ф����ͭ�٥��ȥ������¤٤�Ф褤�����ξ��ˤ�
���Ф����ͭ�٥��ȥ������¤٤�Ф褤�����ξ��ˤ�
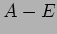 ,
,
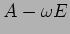 ,
,
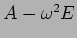 �γˤ����Τ������ᤤ��������
���������������٤ι���ʤ���ܥ٥��ȥ�ιԤ����褯�����
�������ܤΤ��Ǹ�ͭ�٥��ȥ뤬�狼��Ϥ��Ǥ��롣
�ʤ���
�γˤ����Τ������ᤤ��������
���������������٤ι���ʤ���ܥ٥��ȥ�ιԤ����褯�����
�������ܤΤ��Ǹ�ͭ�٥��ȥ뤬�狼��Ϥ��Ǥ��롣
�ʤ���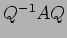 ��
��
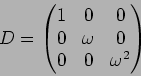
����������)- 4.
- ���
 �ˤ�����
�ˤ�����
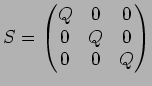 �Ȥ��������ΤȤ�
�Ȥ��������ΤȤ� 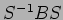 ����ʤ�����
����ʤ�����
����:
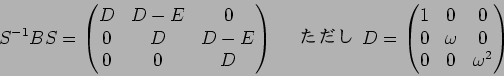
�ȽƤ⤤��������������ʬ��

�ȽƤ�褤���ޤ������Τ褦�˥֥��å���ռ����������Ǥ��ʤ���
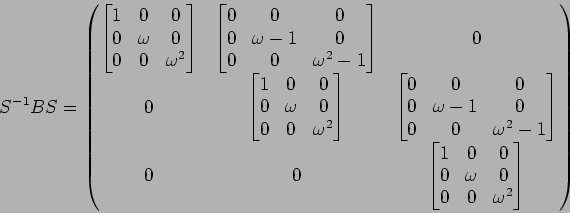
- 5.
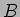 �θ�ͭ�ͤ٤Ƶ��ʤ�����
�θ�ͭ�ͤ٤Ƶ��ʤ�����
����:
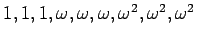 .
.
(
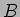 �θ�ͭ������(��ͭ��)��
�θ�ͭ������(��ͭ��)�� 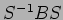 �θ�ͭ������(��ͭ��)�Ϥ��ʤ���)
�θ�ͭ������(��ͭ��)�Ϥ��ʤ���)
- 6.
-
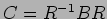 �����������ɸ��ˤʤ�褦��
�����������ɸ��ˤʤ�褦�� 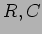 ����ʤ�����
����ʤ�����
����:
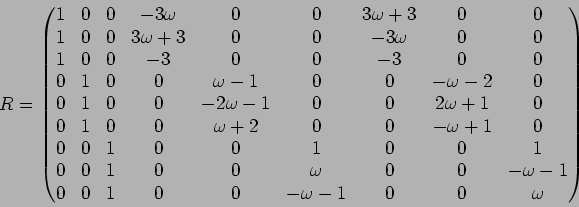
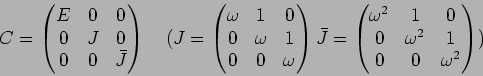
�ޤ�
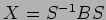 ����٥��ȥ�����ܤ��롣
����٥��ȥ�����ܤ��롣
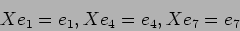
�Ǥ��뤫�顢 �θ�ͭ��
�θ�ͭ��  ���б������ͭ�٥��ȥ�Ȥ���
���б������ͭ�٥��ȥ�Ȥ���
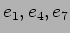 �����뤳�Ȥ��狼�롣Ʊ�ͤˤ��ơ�
�����뤳�Ȥ��狼�롣Ʊ�ͤˤ��ơ�
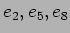 ��
�� 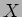 �θ�ͭ��
�θ�ͭ�� 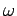 ���б�������ͭ�٥��ȥ�,
���б�������ͭ�٥��ȥ�,
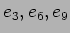 ��
�� 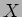 �θ�ͭ��
�θ�ͭ�� 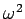 ���б�������ͭ�٥��ȥ�Ǥ��뤳�Ȥ������ˤ狼�롣
���Τ��Ȥ����ܤ��ơ��ҤȤޤ�
���б�������ͭ�٥��ȥ�Ǥ��뤳�Ȥ������ˤ狼�롣
���Τ��Ȥ����ܤ��ơ��ҤȤޤ� 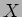 �Τ褦���Ѵ����롣
�Τ褦���Ѵ����롣
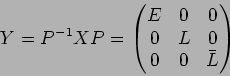
������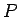 �ϼ��Τ褦�ʴ�����ִ����б��������Ǥ��롣
�ϼ��Τ褦�ʴ�����ִ����б��������Ǥ��롣
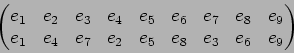
����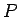 ��
��
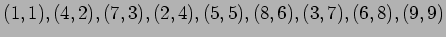 �γ���ʬ
��
�γ���ʬ
�� 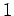 �ǻĤ��
�ǻĤ�� 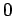 �Ǥ���褦�ʹ���Ǥ��롣
�Ǥ���褦�ʹ���Ǥ��롣
 ���Τ�ΤϤФ��Ф������ΤǤ����Ǥϳ䰦���롣
���Τ�ΤϤФ��Ф������ΤǤ����Ǥϳ䰦���롣
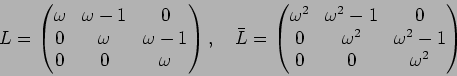
�Ǥ��롣���Ȥ�
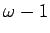 ,
,
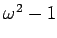 ����ʬ��������뤳�Ȥ�����������ñ�˥٥��ȥ��
���ܤ�����Ф褤��
����ʬ��������뤳�Ȥ�����������ñ�˥٥��ȥ��
���ܤ�����Ф褤��
�������η��ǽҤ٤Ƥ����ȤĤ��Τ褦�ˤʤ롣
���� 6.1(�ʤ�������Υ��������Ƥ�Ʊ�ͤΤ��Ȥ����Ȥ��Ǥ��롣)
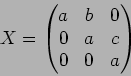
(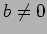 ,
,
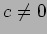 )
�Υ��������ɸ���
)
�Υ��������ɸ���
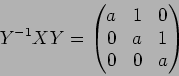
�Ǥ��������롣�����ǡ�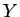 ��
��
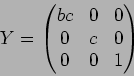
��Ϳ���������Ǥ��롣 - 7.
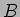 �Υ�������ʬ��ʤ�����
�Υ�������ʬ��ʤ�����
����:
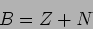
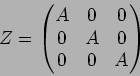

(���줬
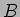 �Υ�������ʬ���Ϳ���뤳�Ȥϡ�����5.1 ��1.-4. �ޤǤν�������
Ĵ�٤�Ф褤������Ϥ䤵����������5.1 �ΰ�����ΰ��ϤǤ��롣)
�Υ�������ʬ���Ϳ���뤳�Ȥϡ�����5.1 ��1.-4. �ޤǤν�������
Ĵ�٤�Ф褤������Ϥ䤵����������5.1 �ΰ�����ΰ��ϤǤ��롣)
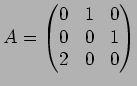 ,
,
![\begin{displaymath}Q=\begin{pmatrix}
1 & 1 & 1 \\
{\sqrt[3]{2}} & {\sqrt[3]{2}}...
...4}} & {\sqrt[3]{4}}\omega^2 & {\sqrt[3]{4}}\omega
\end{pmatrix}\end{displaymath}](img59.png)
![\begin{displaymath}S^{-1}BS
=
\begin{pmatrix}
D & D-E & 0 \\
0 & D & D-E \\
0 ...
...]{2}}\omega & 0 \\
0 & 0 & {\sqrt[3]{2}}\omega^2
\end{pmatrix}\end{displaymath}](img60.png)
![\begin{displaymath}\begin{pmatrix}
{\sqrt[3]{2}} & {\sqrt[3]{2}} -1 & 0 & 0 & 0 ...
...0 & 0 & 0 & 0 & 0 & 0 & {\sqrt[3]{2}} \omega^2\\
\end{pmatrix}\end{displaymath}](img63.png)
![\begin{displaymath}\begin{pmatrix}
-2{\sqrt[3]{2}} + {\sqrt[3]{4}} + 1 & 0 & 0 ...
...{4}} \omega^2
& 0 & 0 & {\sqrt[3]{4}} \omega
\\
\end{pmatrix}\end{displaymath}](img65.png)
![\begin{displaymath}\begin{pmatrix}
{\sqrt[3]{2}} & 1 & 0 & 0 & 0 & 0 & 0 & 0 & ...
... & 0 & 0 & 0 & 0 & 0 & 0 & {\sqrt[3]{2}} \omega^2
\end{pmatrix}\end{displaymath}](img67.png)