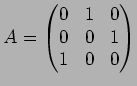 ,
,
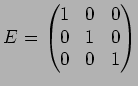 ,
,
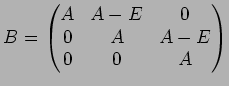 ��������������
��������������
![]() �Ȥ�����
���ΤȤ���
�Ȥ�����
���ΤȤ���
- 1.
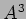 ����ʤ�����
����ʤ�����
- 2.
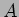 �θ�ͭ�ͤ٤Ƶ��ʤ�����
�θ�ͭ�ͤ٤Ƶ��ʤ�����
- 3.
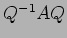 ���гѹ���Ǥ���褦����§����
���гѹ���Ǥ���褦����§���� 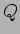 ���ĵ��ʤ�����
���ĵ��ʤ�����
- 4.
- ���
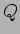 �ˤ�����
�ˤ�����
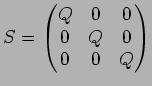 �Ȥ��������ΤȤ�
�Ȥ��������ΤȤ� 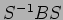 ����ʤ�����
����ʤ�����
- 5.
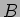 �θ�ͭ�ͤ٤Ƶ��ʤ�����
�θ�ͭ�ͤ٤Ƶ��ʤ�����
- 6.
-
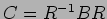 �����������ɸ��ˤʤ�褦��
�����������ɸ��ˤʤ�褦�� 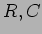 ����ʤ�����
����ʤ�����
- 7.
 �Υ�������ʬ��ʤ�����
�Υ�������ʬ��ʤ�����
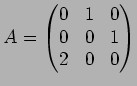 ,
,