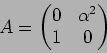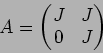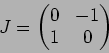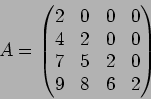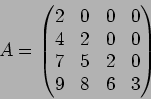�����Υơ���:
![]()
����⡢![]() �Ȥ������Τ�ؤ���ΤȤ��롣
�Ȥ������Τ�ؤ���ΤȤ��롣
��Τ褦��ʬ�� ![]() ��
�� ![]() �� ��������ʬ��(���뤤�� SN ʬ��)
�ȸƤ֡�
�� ��������ʬ��(���뤤�� SN ʬ��)
�ȸƤ֡�
�ʤ���![]() �θ�ͭ�ͤ�
�θ�ͭ�ͤ� ![]() ��°���ʤ��Ƥ⡢
��°���ʤ��Ƥ⡢
![]() �ξ��ʬΥŪ�ʸ��Ф���ʤ顢
�ξ��ʬΥŪ�ʸ��Ф���ʤ顢![]() �Υ�������ʬ���
¸�ߤ����Ȥ��Ǥ��롣
�Υ�������ʬ���
¸�ߤ����Ȥ��Ǥ��롣
�����ϡ����������κ��Ѥ� ![]() �����ѤǤ��뤳�Ȥ�
���դ���д�ñ�Ǥ��롣
�����ѤǤ��뤳�Ȥ�
���դ���д�ñ�Ǥ��롣
��ͭ�ͤ� ![]() ��°���ʤ��褦�ʹ�����Ф��ƥ�������ɸ��ʤɤ����ˤϡ�
��°���ʤ��褦�ʹ�����Ф��ƥ�������ɸ��ʤɤ����ˤϡ�
![]() ��Ŭ���ʳ����Τ�ͤ��Ƥ��Τ��ڤ����������⤤���ʤ����⤢�롣
���������Ȥ��ˤϡ��Ĥ��Τ褦���������Ѥ�������Ω�Ĥ��Ȥ����롣
��Ŭ���ʳ����Τ�ͤ��Ƥ��Τ��ڤ����������⤤���ʤ����⤢�롣
���������Ȥ��ˤϡ��Ĥ��Τ褦���������Ѥ�������Ω�Ĥ��Ȥ����롣
�Ĥ��γ���ˤĤ��ơ��� ![]() �ȹ���
�ȹ���
![]() �ˤ�������
�ˤ�������
![]() �� ��������ʬ��ʤ�����(�Ĥޤꡢ
�� ��������ʬ��ʤ�����(�Ĥޤꡢ![]() ����ʤ�����)
����ʤ�����)