


Next: About this document ...
��������� I ���� No.2
�����Υơ���:

����ϡ�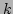 �Ȥ������Τ�ؤ���ΤȤ��롣
�Ȥ������Τ�ؤ���ΤȤ��롣
��� 1
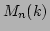
�θ�
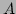
��Ϳ����줿�Ȥ��롣
�⤷
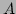
�κǾ�¿�༰�Ȥϡ�
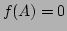
���������褦��
![$f\in k[X]\setminus \{0\}$](img6.png)
�Τ����������Ǿ��Τ�ΤΤ��ȤǤ��롣
���� 2
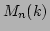
�θ�
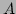
��Ϳ����줿�Ȥ������κǾ�¿�༰��
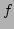
�Ȥ��롣
���ΤȤ���Ǥ�դ�
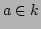
���Ф��ơ�
���ʤꤿ�ġ�
��� 2
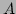
�κǾ�¿�༰
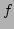
�κ�(��ʣ�Ϲ�θ���ʤ�)��
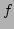
�θ�ͭ�ͤȸƤ֡�
(����)
��ʣ���θ������ͭ�ͤ�����ˤϼ��� Cayley-Hamilton ������
��ɬ�פˤʤ롣
���� 1 (Cayley-Hamilton)
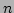
-������������
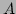
���Ф��ơ����θ�ͭ¿�༰
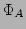
��
��������롣���ΤȤ���
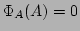
���ʤꤿ�ġ�
���������ξ����ˤĤ��Ƥϼ���˽Ҥ٤롣���������äƺ���(�Υ�ݡ�������)
�Ϥ���������į��� 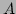 �κǾ�¿�༰�θ�����դ��뤳�Ȥ����������Ƥ���
���Ȥˤ��롣
�κǾ�¿�༰�θ�����դ��뤳�Ȥ����������Ƥ���
���Ȥˤ��롣
ľ��ʬ��ȶ�������δط��ˤĤ����������Ƥ�������
���� 3
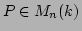
������(
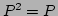
)
�ʤ�С����Τ��Ȥ�����Ω�ġ�
- 1.
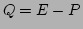 ������Ǥ��ꡢ
������Ǥ��ꡢ
���ʤꤿ�ġ�
- 2.
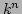 �θ�
�θ� 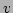 ��
��
�Ȱ��Ū�˽롣(���ʤ����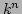 ��
�� 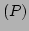 ��
�� 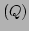 �Ȥ�
ľ�¤Ǥ��롣
�Ȥ�
ľ�¤Ǥ��롣
��� 3
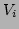
�Τ��Ȥ�
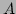
�θ�ͭ��
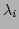
��°������ͭ���֤ȸƤӡ�
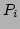
�Τ��Ȥ�
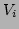
���б�����ͱƤȸƤ֡�
��
���� 2.1
����(ʣ�ǿ�����ʬ�ˤ��)�ƹ���θ�ͭ��(��ʣ�Ϲ�θ���ʤ�)�ȡ�
�����°������ͭ���֤��б�����ͱƤ����Ƶ��衣
- 1.
-
- 2.
-
- 3.
-



Next: About this document ...
Yoshifumi Tsuchimoto
2000-10-21
![]()
![]() �Ȥ������Τ�ؤ���ΤȤ��롣
�Ȥ������Τ�ؤ���ΤȤ��롣
