


Next: About this document ...
����� II ���� No.12
��������  �����Ӥ�����
�����Ӥ�����
 ��
��  �����
�����
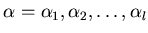 �Ȥ���
�Ȥ���
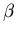 ��
�� 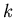 �����
�����
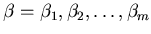 �Ȥ���Ȥ���
�Ȥ���Ȥ���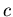 �ϡ�
�ϡ�
�Τɤ�Ȥ�ۤ�褦�����٤Ф褤��
���� 12.1
��
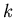
����Ӥ��γ�����
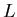
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
��
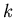
��ޤ�
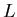
����ʬ�ΤǤ��롣
��� 12.1
��
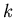
��ͭ�¼�������
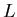
��Ϳ�����Ƥ���Ȥ��롣
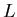
�Τɤθ�
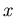
��
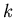
��ʬΥŪ�Ǥ���Ȥ���
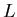
��
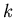
��ʬΥ�����ΤǤ���Ȥ�����
���� 12.2
��
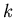
�ȡ�����ͭ�¼����������
![$L=k[\alpha_1,\alpha_2,\dots,\alpha_n]$](img18.png)
��Ϳ�����Ƥ���Ȥ��롣���ΤȤ���
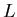
��
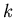
��ʬΥ�����ΤǤ��뤿���
ɬ��ʬ���ϡ�
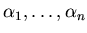
�����٤�
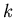
��
ʬΥŪ�Ǥ��뤳�ȤǤ��롣
���� 12.3
̵�¸Ĥθ�������
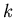
��ͭ�¼�ʬΥ������
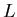
��ɬ��ñ������ΤǤ��롣
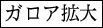
��������ǡ�����ʬΥ����Ǥ����Τ���������Ȥ�����
���� 12.4
��
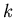
�ȡ�����ͭ�¼�������������
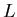
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
���ʤꤿ�ġ�
(����)
���̤ˡ�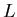 ��
�� 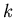 ��ñ�����ʤ�С�
��ñ�����ʤ�С�
������Ω�ĤΤǤ��ä�(���� 8.1)��
�¤ϡ������������� 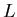 ��
�� 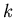 ��ñ�����Ǥʤ��Ȥ⡢���ĤǤ�����Ω�ġ�
����12.3�ȤΤ���
��ñ�����Ǥʤ��Ȥ⡢���ĤǤ�����Ω�ġ�
����12.3�ȤΤ���
���� 12.4
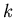
��ͭ�¼�������
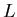
����
��ߤ����ʤ�С�
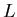
��
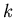
�Υ���������Ǥ��뤳�Ȥ��ʤ�����



Next: About this document ...
Yoshifumi Tsuchimoto
2000-07-03
![]()
![]() �����Ӥ�����
�����Ӥ�����
![]() ��
�� ![]() �����
�����
![]() �Ȥ���
�Ȥ���
![]() ��
�� ![]() �����
�����
![]() �Ȥ���Ȥ���
�Ȥ���Ȥ���![]() �ϡ�
�ϡ�
![]()
![]() ��
�� ![]() ��ñ�����ʤ�С�
��ñ�����ʤ�С�