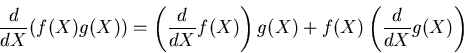Next: About this document ...
����� II ���� No.11

��� 11.1
��

�Ȥ��γ�����
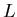
��Ϳ�����Ƥ���Ȥ��롣

�����Ū�ʸ�
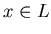
��Ϳ�����Ƥ���Ȥ���
����

��κǾ�¿�༰��
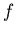
�Ȥ��롣
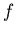
���ź���⤿�ʤ��Ȥ���
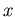
��

��ʬΥŪ�Ǥ���Ȥ�����
(����)
�������Τ褦�ˡ�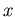 �����äƤ��������
�����äƤ�������� 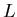 ��(����Ū�ˤ�ɬ�פ���)
�����ƽ��פǤʤ���礬���롣�ʲ��ǤϤ��Τ褦�ʤȤ��ˤϡ�
��(����Ū�ˤ�ɬ�פ���)
�����ƽ��פǤʤ���礬���롣�ʲ��ǤϤ��Τ褦�ʤȤ��ˤϡ�
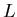 �����Τ˽���ñ�� ��
�����Τ˽���ñ�� �� �����Ū�ʸ�
�����Ū�ʸ� 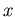 �פǤ��ޤ����Ȥˤ��롣
�פǤ��ޤ����Ȥˤ��롣
���� 11.1
��

���¿�༰
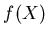
������
![$k[X]$](img8.png)
�θ�
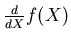
��
����Ū������Ǥ��롣
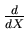
��

-�����ǡ�
����������
�� 11.1
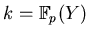
���¿�༰
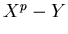
���

����ʬΥŪ�Ǥ��롣
�� 11.1
��

�ȡ�

�����Ū�ʸ�
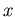
�����ä��Ȥ��롣
�⤷

��ɸ����
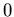
�ʤ�С�
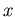
��

��ʬΥŪ�Ǥ��롣
�⤷

��ͭ���Τʤ�С�
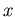
��

��ʬΥŪ�Ǥ��롣
���� 11.1
��

����Ӥ��γ�����
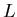
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
��

��ޤ�
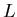
����ʬ�ΤǤ��롣
��� 11.2
��

��ͭ�¼�������
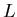
��Ϳ�����Ƥ���Ȥ��롣
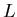
�Τɤθ�
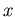
��

��ʬΥŪ�Ǥ���Ȥ���
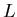
��

��ʬΥ�����ΤǤ���Ȥ�����
���� 11.2
��

�ȡ�����ͭ�¼����������
![$L=k[\alpha_1,\alpha_2,\dots,\alpha_n]$](img28.png)
��Ϳ�����Ƥ���Ȥ��롣���ΤȤ���
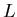
��

��ʬΥ�����ΤǤ��뤿���
ɬ��ʬ���ϡ�
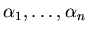
�����٤�

��
ʬΥŪ�Ǥ��뤳�ȤǤ��롣
���� 11.3
̵�¸Ĥθ�������

��ͭ�¼�ʬΥ������
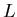
��ɬ��ñ������ΤǤ��롣
��������ǡ���̵�¸Ĥθ����ġפȤ���  �ξ��ϤϤ������Ȥ��Ǥ��롣
����11.3�ȤΤ��ȡ�
�ξ��ϤϤ������Ȥ��Ǥ��롣
����11.3�ȤΤ��ȡ�
���� 11.1
�Ĥ���
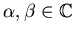
�ˤ������ơ�
![$\mbox{${\Bbb Q}$ }[\alpha,\beta]=\mbox{${\Bbb Q}$ }[c\alpha+\beta]$](img31.png)
�Ȥʤ�褦��
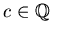
�줾����ʤ�����(��ͳ��ź���뤳�ȡ�)
- 1.
-
![$\alpha=\sqrt[3]{5},\quad \beta=\sqrt[3]{5}\omega$](img33.png)
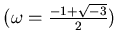
- 2.
-
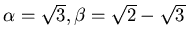
����˾�γ���ˤĤ��ơ�
![$\mbox{${\Bbb Q}$ }[\alpha+\beta]=\mbox{${\Bbb Q}$ }[\alpha,\beta]$](img36.png)
���ʤꤿ�Ĥ��ɤ���Ĵ�٤ʤ�����(��ͳ��ź���뤳�ȡ�)



Next: About this document ...
Yoshifumi Tsuchimoto
2000-06-26
![]()
![]() �����äƤ��������
�����äƤ�������� ![]() ��(����Ū�ˤ�ɬ�פ���)
�����ƽ��פǤʤ���礬���롣�ʲ��ǤϤ��Τ褦�ʤȤ��ˤϡ�
��(����Ū�ˤ�ɬ�פ���)
�����ƽ��פǤʤ���礬���롣�ʲ��ǤϤ��Τ褦�ʤȤ��ˤϡ�
![]() �����Τ˽���ñ�� ��
�����Τ˽���ñ�� ��![]() �����Ū�ʸ�
�����Ū�ʸ� ![]() �פǤ��ޤ����Ȥˤ��롣
�פǤ��ޤ����Ȥˤ��롣