


Next: About this document ...
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ II ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ No.8

๏ฟฝ๏ฟฝ๏ฟฝ 8.1
๏ฟฝ๏ฟฝ
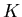
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
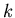
๏ฟฝ๏ฟฝรฑ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๏ฟฝศคฯก๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
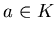
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝรค๏ฟฝ
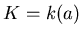
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤคศค๏ฟฝ๏ฟฝหธ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝโคท๏ฟฝ๏ฟฝ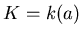 ๏ฟฝวก๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝวก๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 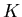 ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ 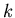 ๏ฟฝ๏ฟฝอญ๏ฟฝยผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝะก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝวคหฝาคูค๏ฟฝ๏ฟฝ่คฆ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝอญ๏ฟฝยผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝะก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝวคหฝาคูค๏ฟฝ๏ฟฝ่คฆ๏ฟฝ๏ฟฝ ![$K=k[a]$](img6.png) ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 8.1
๏ฟฝ๏ฟฝ
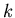
๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝอญ๏ฟฝยผ๏ฟฝรฑ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
![$K=k[a]$](img6.png)
๏ฟฝ๏ฟฝอฟ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฦค๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๋กฃ
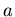
๏ฟฝ๏ฟฝ
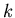
๏ฟฝ๏ฟฝฮบวพ๏ฟฝยฟ๏ฟฝเผฐ๏ฟฝ๏ฟฝ
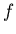
๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮค๏ฟฝ๏ฟฝศค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ
- 1.
-
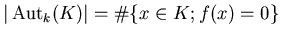 .
.
- 2.
-
![$\vert\operatorname{Aut}_k(K)\vert\leq \deg(f)\leq [K:k]$](img10.png)
๏ฟฝ๏ฟฝ๏ฟฝฮป๏ฟฝ๏ฟฝฤค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮปฤค๏ฟฝวค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ 8.1
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2}])=1.$](img11.png)
๏ฟฝ๏ฟฝ 8.2
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])=\frak{S}_3$](img12.png)
(๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝะพฮท๏ฟฝ).
๏ฟฝ๏ฟฝ 8.3
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }[\omega]}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])={\mbox{${\Bbb Z}$ }}/3{\mbox{${\Bbb Z}$ }}$](img13.png)
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 8.1
๏ฟฝ๏ฟฝ๏ฟฝฤค๏ฟฝ๏ฟฝ๏ฟฝ
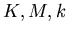
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝรคฦก๏ฟฝ
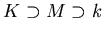
๏ฟฝ๏ฟฝ๏ฟฝสค๊คฟ๏ฟฝฤคศค๏ฟฝ๏ฟฝ๏ฟฝ
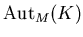
๏ฟฝ๏ฟฝ
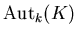
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสฌ๏ฟฝ๏ฟฝ๏ฟฝวค๏ฟฝ๏ฟฝ๋กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 8.1
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[4]{5}])$](img18.png)
๏ฟฝฮฐฬฟ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ่กฃ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ 8.2
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2+\sqrt{3}}])$](img19.png)
๏ฟฝฮฐฬฟ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ่กฃ
Yoshifumi Tsuchimoto
2000-06-06
![]()
![]() ๏ฟฝวก๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ
๏ฟฝวก๏ฟฝ๏ฟฝสค๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ ![]() ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝ ![]() ๏ฟฝ๏ฟฝอญ๏ฟฝยผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝะก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝวคหฝาคูค๏ฟฝ๏ฟฝ่คฆ๏ฟฝ๏ฟฝ
๏ฟฝ๏ฟฝอญ๏ฟฝยผ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝสค๏ฟฝะก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝวคหฝาคูค๏ฟฝ๏ฟฝ่คฆ๏ฟฝ๏ฟฝ ![]() ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ
๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝ๏ฟฝฮฉ๏ฟฝฤก๏ฟฝ