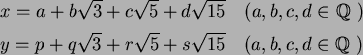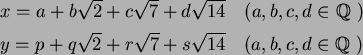Next: About this document ...
����� II ���� No.7

��� 7.1 (���6.3�κƷ�)
��
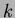
�Ȥ��γ�����
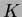
��Ϳ�����Ƥ���Ȥ��롣
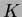
��
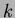
����Ʊ��(���뤤�ϡ�
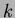
��μ���Ʊ��)�Ȥϡ�
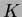
����
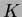
�ؤ�Ʊ��
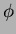
�Ǥ��äơ�
Ǥ�դ�
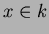
������
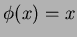
������Ω�Ĥ�Τ������
���� 7.1
��
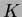
�Ȥ�����ʬ��
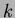
��Ϳ�����Ƥ��ơ�
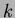
���
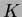
�μ���Ʊ��
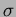
�����ä��Ȥ��롣���ΤȤ���
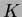
��Ǥ�դθ�
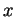
���Ф��ơ�
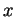
��
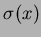
�Ȥ϶���Ǥ��롣
���������ˤ��ơ�Ϳ����줿�Τ��ɤΤ��餤����Ʊ�����Ĥ�����Ǥ��롣
�� 7.1
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img10.png)
��
��μ���Ʊ�����ɤΤ��餤���뤫���Ƥߤ褦��
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img10.png)
��
��μ���Ʊ���ΰ�Ĥ�
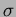
�Ȥ���ȡ�
��������ˤ�ꡢ
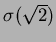
��
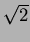
��
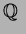
��
����Ǥʤ��ƤϤʤ�ʤ���
���Τ��Ȥ��顢
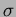
�ϼ�����ĤΤɤ��餫�����ʤ����Ȥ��狼�롣
- 1.
-
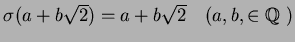 (��������)
(��������)
- 2.
-
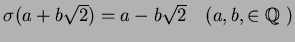
���� 7.1
��
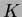
�Ȥ�����ʬ��
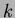
��Ϳ�����Ƥ���Ȥ��롣
���ΤȤ���
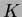
��
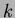
��μ���Ʊ�����Τ�(������Ʊ���˴ؤ���)����ʤ���
��� 7.2
���������
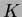
��
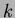
��μ���Ʊ�����Ȥ�����
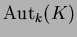
�Ƚ���魯��
���� 7.2
�⤷
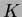
��
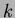
��ĤȤ���
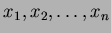
����������Ƥ���ʤ�С�
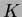
��
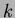
��μ���Ʊ��
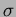
��

��
��äư�դ˷�ޤ롣
����:��������``�ĤȤ���''�Ƚ���ʬ��``�ΤȤ���''���֤������Ƥ�
�������Ω���롣�����μ�֤�ۤܤ����ʤ���
�������ȡ�����7.1 ���Ѥ���ȡ��Τμ���Ʊ�����ɤΤ��餤���뤫
���������狼�롣
�� 7.2
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2}])\cong{\mbox{${\Bbb Z}$ }}/2{\mbox{${\Bbb Z}$ }}.$](img19.png)
�� 7.3
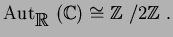
�� 7.4
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{5}])\...
... Z}$ }}/2{\mbox{${\Bbb Z}$ }}\times {\mbox{${\Bbb Z}$ }}/2{\mbox{${\Bbb Z}$ }}.$](img21.png)
�� 7.5
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2}])=1.$](img22.png)
��������(���������)�Ǥϡ�
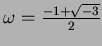 �Ȥ�����
�Ȥ�����
�� 7.6
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])=\frak{S}_3$](img24.png)
(�����оη�).
�� 7.7
![$\operatorname{Aut}_{\mbox{${\Bbb Q}$ }[\omega]}(\mbox{${\Bbb Q}$ }[\sqrt[3]{2},\omega])={\mbox{${\Bbb Z}$ }}/3{\mbox{${\Bbb Z}$ }}$](img25.png)
(�����оη�).
�����Ǥ⸫����褦�ˡ�����Ʊ����������鼡�Τ��Ȥ�����Ω�Ĥ��Ȥ��狼�롣
���� 7.3
���Ĥ���
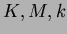
�����äơ�
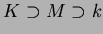
���ʤꤿ�ĤȤ���
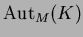
��
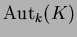
����ʬ���Ǥ��롣
����ϡ�����7.1 �Ͻ����ֹ椬����ֹ�ο��ѡ�
����7.2 �Ͻ����ֹ椬�����ֹ�ο��ѤȤ��롣(7.3,7.4�ˤϤȤ������¤�
�ʤ���â������ʤ������)
���� 7.1
![$\mbox{${\Bbb Q}$ }[\sqrt{3},\sqrt{5}]$](img29.png)
��
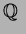
��μ���Ʊ��
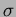
����
�����������Ȥ��롣���ΤȤ���
![$\mbox{${\Bbb Q}$ }[\sqrt{3},\sqrt{5}]$](img29.png)
�θ�
��
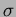
�ˤ�äƤɤΤ褦�ʸ��˼̤���뤫(
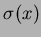
�Ϥ����餫)
�Ҥ٤衣����ˡ�����
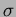
�ϼºݤ�
��ߤ������Ȥ�
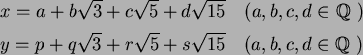
�Ȥ����ƳΤ���Ƥߤ衣
���� 7.2
![$\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{7}]$](img34.png)
��
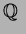
��μ���Ʊ��
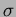
����
�����������Ȥ��롣���ΤȤ���
![$\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{7}]$](img34.png)
�θ�
��
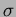
�ˤ�äƤɤΤ褦�ʸ��˼̤���뤫(
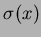
�Ϥ����餫)
�Ҥ٤衣����ˡ�����
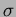
�ϼºݤ�
��ߤ������Ȥ�
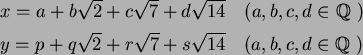
�Ȥ����ƳΤ���Ƥߤ衣



Next: About this document ...
Yoshifumi Tsuchimoto
2000-06-05
![]()
![]() �Ȥ�����
�Ȥ�����