


Next: About this document ...
����� II ���� No.6

��� 6.1
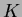
����
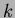
��
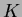
����ʬ�ΤȤ��롣���ΤȤ���
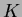
��
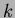
�δ֤�
����ΤȤϡ�
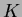
����ʬ�Τǡ�
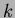
��ޤ��ΤΤ��ȤǤ��롣
�� 6.1
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img4.png)
��
![$\mbox{${\Bbb Q}$ }[\sqrt{2},\sqrt{3}]$](img5.png)
��
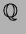
�Ȥ�
�֤�����ΤǤ��롣
����Τޤ��Ѥ���ȡ�¿�༰�δ����������꤬�䤵�����ʤ��礬���롣

��� 6.2
��
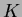
�Ȥ�����ʬ��
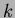
��Ϳ�����Ƥ���Ȥ��롣
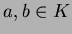
��
���ä��Ȥ���
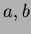
��
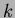
��ζ��Ǥ���Ȥϡ�
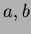
��
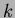
�����Ū�Ǥ��äơ�
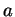
,
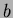
��
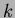
��κǾ�¿�༰�� (����ܤ������)���פ���Ȥ��˸�����
���� 6.1
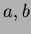
��
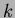
�嶦��ʤ�С��ΤȤ��Ƥ�Ʊ��
![$k[a]\cong k[b]$](img20.png)
��¸�ߤ��롣
�� 6.4
�ͤĤθ�
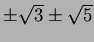
�Ϥɤ���Ĥ�ߤ���
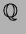
�嶦��Ǥ��롣
�� 6.5
![$\sqrt[3]{5}$](img24.png)
��
![$\sqrt[3]{5}\omega$](img25.png)
(�
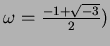
)
�Ȥ�
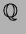
��ߤ��˶���Ǥ��뤬��
![$\mbox{${\Bbb Q}$ }[\sqrt[3]{5}]$](img27.png)
��Ǥ���Ĥ϶���ǤϤʤ���
��� 6.3
��
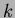
�Ȥ��γ�����
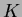
��Ϳ�����Ƥ���Ȥ��롣
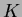
��
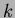
����Ʊ��(���뤤�ϡ�
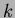
��μ���Ʊ��)�Ȥϡ�
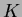
����
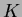
�ؤ�Ʊ��
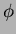
�Ǥ��äơ�
Ǥ�դ�
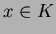
������
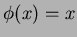
������Ω�Ĥ�Τ������
�� 6.6
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img4.png)
���餽�켫�Ȥؤν�Ʊ��
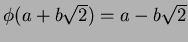
��
![$\mbox{${\Bbb Q}$ }[\sqrt{2}]$](img4.png)
��
��� ����Ʊ���Ǥ��롣
���̤ˡ��� 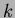 ���� ¾����
���� ¾���� 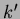 �ؤ�Ʊ��
�ؤ�Ʊ��
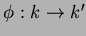 ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���
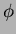 ��Ĥ��Τ褦��
��Ĥ��Τ褦�� ![$k[X]$](img34.png) ����
���� ![$k'[X]$](img35.png) �ؤ�Ʊ���˿��Ф����Ȥ��Ǥ��롣
����ιֵ��Ǥϲ���
�ؤ�Ʊ���˿��Ф����Ȥ��Ǥ��롣
����ιֵ��Ǥϲ��� 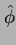 �Ȥ������Ȥˤ��롣(����Ū�ʵ���ǤϤʤ���)
�Ȥ������Ȥˤ��롣(����Ū�ʵ���ǤϤʤ���)
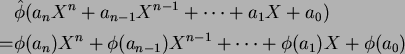
���� 6.2
��
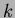
�ȡ����γ�����
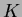
��Ϳ�����Ƥ��ơ������
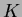
��
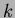
��μ���Ʊ��
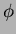
��Ϳ�����Ƥ���Ȥ��롣
�⤷
![$f\in k[X]$](img38.png)
,
![$g\in K[X]$](img39.png)
�����äơ�
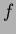
��(
![$K[X]$](img40.png)
�Τʤ���)
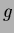
�dz���ڤ��С�
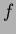
�� (
![$K[X]$](img40.png)
�Τʤ���)
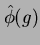
�Ǥ����ڤ�롣
�����������Ѥ���С���6.2�� 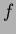 �δ������Ϥ�äȴ�ñ�˼������Ȥ��Ǥ��롣
�δ������Ϥ�äȴ�ñ�˼������Ȥ��Ǥ��롣
���� 6.2
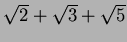
��
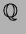
��κǾ�¿�༰���ᡢ
�ºݤˤ��줬����Ǥ��뤳�Ȥ��ʤ�����
Yoshifumi Tsuchimoto
2000-05-23
![]()
![]()
![]() ���� ¾����
���� ¾���� ![]() �ؤ�Ʊ��
�ؤ�Ʊ��
![]() ��Ϳ�����Ƥ���Ȥ���
��Ϳ�����Ƥ���Ȥ���
![]() ��Ĥ��Τ褦��
��Ĥ��Τ褦�� ![]() ����
���� ![]() �ؤ�Ʊ���˿��Ф����Ȥ��Ǥ��롣
����ιֵ��Ǥϲ���
�ؤ�Ʊ���˿��Ф����Ȥ��Ǥ��롣
����ιֵ��Ǥϲ��� ![]() �Ȥ������Ȥˤ��롣(����Ū�ʵ���ǤϤʤ���)
�Ȥ������Ȥˤ��롣(����Ū�ʵ���ǤϤʤ���)
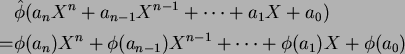
![]() �δ������Ϥ�äȴ�ñ�˼������Ȥ��Ǥ��롣
�δ������Ϥ�äȴ�ñ�˼������Ȥ��Ǥ��롣
![]() ��
��
![]() ��κǾ�¿�༰���Ȥᡢ
�ºݤˤ��줬����Ǥ��뤳�Ȥ��ʤ�����
����ˡ�
��κǾ�¿�༰���Ȥᡢ
�ºݤˤ��줬����Ǥ��뤳�Ȥ��ʤ�����
����ˡ�
![]() �ȶ����
�ȶ���� ![]() �θ��٤�
��Ȥ�ʤ�����
�θ��٤�
��Ȥ�ʤ�����
![]() ��
��
![]() ��κǾ�¿�༰���Ȥᡢ
�ºݤˤ��줬����Ǥ��뤳�Ȥ��ʤ�����
����ˡ�
��κǾ�¿�༰���Ȥᡢ
�ºݤˤ��줬����Ǥ��뤳�Ȥ��ʤ�����
����ˡ�
![]() �ȶ����
�ȶ���� ![]() �θ��٤�
��Ȥ�ʤ�����
�θ��٤�
��Ȥ�ʤ�����