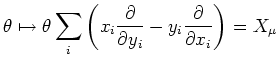
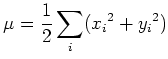
![]() の各 fiber は
の各 fiber は ![]() 次元球面であり、それを
次元球面であり、それを ![]() で割れば
1.節のものと同じ
で割れば
1.節のものと同じ
![]() を得ることになる。
を得ることになる。
良く知られているように、複素多様体においては、メトリックとシンプレクティック
形式がうまく対応づけられることがある。(このような多様体を
ケーラー多様体と呼ぶ。)
ケーラー多様体にリー群が作用していて、その作用が複素構造および
シンプレクティック構造を保つなら、そのシンプレクティック 商 も
ケーラー多様体であることがわかる。今の例はその典型であって、
それを用いて
![]() はケーラー多様体であり、計量が定まることがわかる。
それが Fubini-Study 計量 である。
はケーラー多様体であり、計量が定まることがわかる。
それが Fubini-Study 計量 である。