

: シンプレクティック 商
: 複素射影空間
: シンプレクティック多様体とポアソン括弧
非可換環 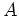 (unital, associative)に対して、
(unital, associative)に対して、
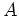 が十分多くのイデアルを持つことは余り期待できない。
比較的簡単に作れるのは
が十分多くのイデアルを持つことは余り期待できない。
比較的簡単に作れるのは 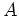 の片側イデアルであって、
たとえば左イデアルなら
の片側イデアルであって、
たとえば左イデアルなら 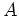 のいくつかの元
のいくつかの元 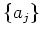 をとって、
をとって、
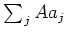 を考えれば良い。
そこで、この節では
を考えれば良い。
そこで、この節では 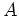 の左イデアル
の左イデアル 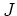
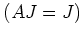 に対して、
に対して、
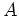 を
を 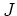 で「制限」するということを考える。
で「制限」するということを考える。
まず、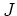 のイデアル化子 (idealizer)
のイデアル化子 (idealizer) 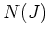 を、
を、
で定める。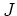 は
は 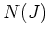 のなかではイデアルである。
そこで、次のような代数を考えることができる。
この
のなかではイデアルである。
そこで、次のような代数を考えることができる。
この 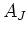 のことを
のことを 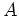 の
の 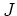 による「制限」とよぶことにする。
による「制限」とよぶことにする。
(例)
上の例は、次のように説明できる。
ある粒子の第 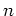 座標が 0 である (
座標が 0 である (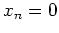 ) ということが
(例えば観測の結果)わかったとする。
不確定性原理によって、そのようなときには
) ということが
(例えば観測の結果)わかったとする。
不確定性原理によって、そのようなときには 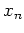 の共役運動量である
の共役運動量である
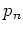 は全く不確定になってしまう。
そこで、
は全く不確定になってしまう。
そこで、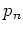 を放棄して、
を放棄して、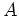 の変わりにその部分代数である
の変わりにその部分代数である 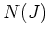 をとり、
をとり、
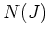 を
を 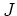 で割ってしまおうというわけである。
で割ってしまおうというわけである。
この議論を一般化すると、
環 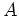 の
の
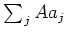 による「制限」とは、考えを
による「制限」とは、考えを 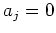 に制限するために、
に制限するために、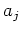 と同時観測可能でない変数を捨てる、
ということをしていることがわかる。
と同時観測可能でない変数を捨てる、
ということをしていることがわかる。
上の例で、座標と微分の役割を入れ換えて考えると、
実は部分環をとる操作と商環をとる操作は互いに裏腹の関係にあることがはっきりして、
もう一つの面白い考え方が生じる。以下それを詳しく見てみよう。
(例2)
この例は、次のように説明できる。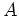 から、
から、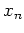 という変数を落として、
という変数を落として、
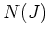 を得ることは、考えている空間を
を得ることは、考えている空間を 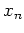 軸に沿う「フロー」で
割ることを意味しており、
軸に沿う「フロー」で
割ることを意味しており、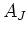 を
を 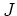 で割ることは、
フローに対応する「モーメント」が一定であるとみていることになる。
で割ることは、
フローに対応する「モーメント」が一定であるとみていることになる。
この節を終える前に一つ注意をしておこう。
一般に、環 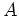 の部分環や商環を考える際には
の部分環や商環を考える際には 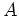 の元が少なすぎることによる
「欠陥」が生じることがあり、それを補うためには
ホモロジー代数的な考察を行うのが普通である。
そのことについては super 変数の導入までしばらくおいておくことにし、
以下では基本的に「とてもよい」場合のみを考えることにする。
の元が少なすぎることによる
「欠陥」が生じることがあり、それを補うためには
ホモロジー代数的な考察を行うのが普通である。
そのことについては super 変数の導入までしばらくおいておくことにし、
以下では基本的に「とてもよい」場合のみを考えることにする。


: シンプレクティック 商
: 複素射影空間
: シンプレクティック多様体とポアソン括弧
平成16年8月24日
![]() のイデアル化子 (idealizer)
のイデアル化子 (idealizer) ![]() を、
を、
![]() の
の
![]() による「制限」とは、考えを
による「制限」とは、考えを ![]() に制限するために、
に制限するために、![]() と同時観測可能でない変数を捨てる、
ということをしていることがわかる。
と同時観測可能でない変数を捨てる、
ということをしていることがわかる。
![]() の部分環や商環を考える際には
の部分環や商環を考える際には ![]() の元が少なすぎることによる
「欠陥」が生じることがあり、それを補うためには
ホモロジー代数的な考察を行うのが普通である。
そのことについては super 変数の導入までしばらくおいておくことにし、
以下では基本的に「とてもよい」場合のみを考えることにする。
の元が少なすぎることによる
「欠陥」が生じることがあり、それを補うためには
ホモロジー代数的な考察を行うのが普通である。
そのことについては super 変数の導入までしばらくおいておくことにし、
以下では基本的に「とてもよい」場合のみを考えることにする。