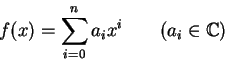
前節では、古典論と量子論の「対応」、 とくに通常の関数に微分作用素等の「作用素」 を対応させる話が出た。 このような「対応」のためには作用素の非可換性以外にも 解決されるべき問題がいくつかある。 このあたりの事情について少し触れておこう。
まずこのような「対応」の多くがしばしば「代入算」として 説明されることに注意しておく。 実際、関数はしばしば多項式の「極限」として得られ、 多項式については(作用素の積の順序の問題を別にすれば) 前節で述べたような「対応」を容易につけることができる。
議論に現れる作用素が一つだけの時には、この対応はとくに見やすい。
多項式
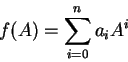
○自己共役な作用素に対する代入算
ヒルベルト空間 H 上の作用素 A が自己共役なら、A を
![]() 上の任意の連続関数 f に代入することができる。
上の任意の連続関数 f に代入することができる。
大学初年級の知識で、このことをある程度了解するために、 H が有限次元の時を考えてみることにしよう。 このときには、 A はユニタリ作用素で対角化される。 f(A) を求めるには A を対角化して対角線の各要素を f に代入すればいい。 もう少し詳しくいうと、次のようになる。
A が次のように対角化されているとする。
(U はユニタリ行列。D は対角行列。)
このとき、任意の一変数多項式 f(x) に対して、
H が無限次元の時には、上の「対角化」は「スペクトル測度」 による「スペクトル分解」に置き換えることになる。 有限次元の時のように「対角要素」(スペクトル)は離散的に現れるとは限らず、 いわゆる「連続スペクトル」を考慮にいれなければならなくなる。 その結果さすがに全ての関数 f に作用素 A を代入するわけにはいかなくなるが、 f のボレル可測性を仮定すれば f(A) を定義することができる。 (我々が普通に考える関数は大抵ボレル可測である。)
上の議論でも察しがつくように、 f(A) は A のスペクトル集合 Sp(A) 上での f の値にのみ依存する。
代入算は Sp(A) 上の関数環と、A で「位相的に生成された」作用素代数との 環としての同型を与える。作用素代数の種々の問題が集合 Sp(A) の 問題に帰着されるのである。
作用素の数が増えた時にも、これらの作用素が互いに可換であるならば、 上のような議論が可能である。(線型代数の知識では、 「可換な対称行列は同時対角化可能」という定理がこれにあたる。)
例えば、Gel'fand による可換 C* 代数の表現定理:
- 可換 C* 代数はあるコンパクト集合 K 上の 連続関数全体のなす環と同型である。 -
はこのタイプの定理の代表的なものである。
可換環にその「スペクトル集合」を対応させるというアイディアは、 補強されてアファインスキームの理論につながっていくことになる。 これについては代数幾何学の成書を参照されたい。
○一般の作用素に対する代入算
上の議論で、「自己共役な」作用素について考察してみたが、 一般の作用素についてはどうであろうか。
A が正規、すなわち A とその共役作用素 A* とが可換な場合には、 容易に上の議論に帰着できる。A* が重要視されるのは、 Weierstrass の多項式近似定理(の複素領域版)
-
複素平面 ![]() の任意のコンパクトな部分集合 K と
その上の連続関数 f は,
の任意のコンパクトな部分集合 K と
その上の連続関数 f は, ![]() の多項式で K 上一様に
近似できる。
-
の多項式で K 上一様に
近似できる。
-
にその源を求めることができる。(z の複素共役 ![]() が
必要になる所がポイントである。)
が
必要になる所がポイントである。)
z のみの多項式で近似できるのは K の内部で解析的な関数のみであり、
それに対応して
正規と限らない作用素 A はそのスペクトル集合の近傍で解析的な関数
には代入できることが示される。
(線型代数の知識でいえば、A は「対角化可能部分」S と「巾零部分」 Nの和(で、S と N は可換)というぐあいに書け、
f の Taylor展開を用いて
なお、この節で述べたことは、 Bourbaki(本家!) 「スペクトル論」に詳しい。