$k$ -rationality

PROPOSITION 4.13   Let $A$ be a square matrix over a field $k$ . Let

$$A=S+N$$

be the Jordan-Chevalley decomposition of $A$ .

Let $m_A$ be the minimal polynomial of $A$ . If all of the roots of $m_A$ are separable over $k$ , then $S$ and $N$ are defined over $k$ . (That means, they are matrices over $k$ ).

PROOF.. In view of Corollary , we may assume that $m_A$ is of the form $f^e$ for some irreducible polynomial $f$ and a positive integer $e$ . By assumption, $f$ has only simple roots.

$$f(X)=\prod_{j=1}^d (X-c_j)$$

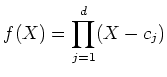
Let us define a polynomial $\chi_s(X) \in \overline{k}[X]$ as follows.

$$\chi_s(X)= \frac {\prod_{{1\leq j \leq d}\atop {j\neq s}} (X-c_j)} {\prod_{{1\leq j \leq d}\atop {j\neq s}} (c_s-c_j)} \qquad (s=1,2,3,\dots,d)$$

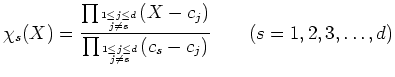
These polynomials are designed to satisfy the following property.

$$\chi_s(c_j)= \begin{cases} 1 & \text{ if }j=s\\ 0 & \text{ if }j\neq s \end{cases}$$

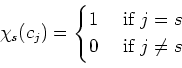
Then we further define

$$\phi_s^{(e)}(X)=1-(1-\chi_s^e)^e$$

and

$$\psi(X)=\sum_{s=1}^{d} c_s \phi_s^{(e)}(X).$$

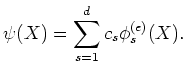
It is fairly easy to see that

$$S=\psi(A)$$

holds.

The function $\psi$ is symmetric with respect to roots $\{c_s\}$ and thus $\psi$ is a polynomial with coefficients in $k$ . Thus $S$ (hence also $N$ ) is defined over $k$ .

$\qedsymbol$

The following example shows that the $k$ -rationality of $S$ does not necessarily hold when we drop off the assumption on $A$ .

EXAMPLE 4.14   Let $A\in M_p(\mathbb{F}_p(x))$ be a matrix of the following form.

$$A= \begin{pmatrix} 0& 1 &\\ & \ddots & \ddots\\ & &\ddots& 1 \\ x& & & 0 \end{pmatrix}$$

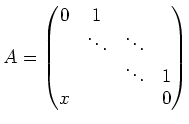
Then the minimal polynomial of $A$ is given by $X^p-x$ . The Jordan-Chevalley decomposition of $A$ is given by

$$A=x^{1/p}+(A-x^{1/p}).$$

Thus the decomposition is not defined over $\mathbb{F}_p(x)$ .