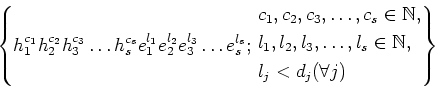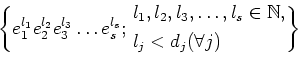

Next: Cartan's criterion for solvability(Ccs)
Up: generalities in finite dimensional
Previous: functoriality of Killing forms
THEOREM 5.28
Let  be a Lie algebra over a field
be a Lie algebra over a field  of characteristic
of characteristic 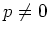 .
Then
.
Then  has a finite dimensional faithful representation.
More precisely, there exists a two-sided ideal
has a finite dimensional faithful representation.
More precisely, there exists a two-sided ideal 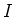 of the universal
enveloping algebra
of the universal
enveloping algebra 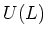 such that
such that  acts faithfully on
acts faithfully on 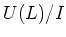 .
.
Before proving the above theorem, we first prove the next lemma.
LEMMA 5.29
Under the hypothesis of the theorem, for any 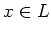 , there exists
a monic non constant polynomial
, there exists
a monic non constant polynomial
![$ f_x(X) \in k[X]$](img387.png) such that
such that
holds.
PROOF..
Let us put
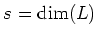
.
The linear transformation
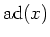
on

is represented by a matrix of
size
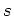
and has therefore its minimal polynomial
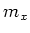
:
Namely,
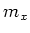
is a monic polynomial of degree no more than
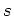
such that
holds.
Let us divide
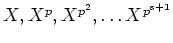
by
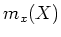
.
Then
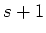
polynomials
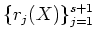
of degree
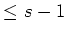
should be linearly dependent. That
means, there exists a non trivial vector
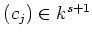
such that
holds. Then we have
Thus we conclude
By dividing
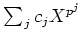
by leading coefficient, we obtain the
required polynomial
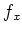
.
PROOF..
of the Theorem
Let
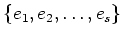
be a basis of

. Then by the above lemma
we know that there exists a set of
monic non constant polynomials
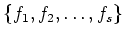
such that each
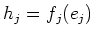
belongs to the center of
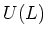
.
Let us put
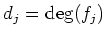
. Then using PWB theorem we may
easily see that
forms a basis of
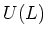
.
Let us now put
Then
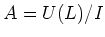
is a finite dimensional vector space with the base
The representation
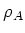
of

on
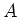
is faithful.
Indeed, for any
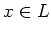
, we have
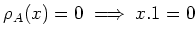
in
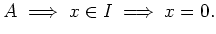
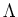
The following remark is (at least) in the Book of Bourbaki.
PROPOSITION 5.31
Let  be a non zero finite dimensional Lie algebra
over a field
be a non zero finite dimensional Lie algebra
over a field 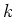 of characteristic
of characteristic 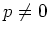 .
Then
.
Then  can never be completely reducible.
can never be completely reducible.
PROOF..
Let us follow the proof of the theorem of Iwasawa.
By taking
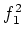
instead of
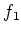
in the proof, we obtain a representation
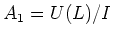
with a non trivial central nilpotent
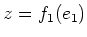
.
Then we see that
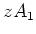
cannot have a direct complementary

-module
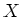
.
For if it existed, then
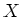
should necessarily a left ideal of
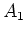
.
On the other hand, by decomposing
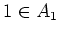
we obtain
Then
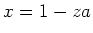
has an inverse
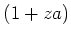
. This implies that
which is a contradiction.


Next: Cartan's criterion for solvability(Ccs)
Up: generalities in finite dimensional
Previous: functoriality of Killing forms
2009-03-06
![$\displaystyle \sum_j c_j X^{p^j}\in m_x(X) k[X]
$](img400.png)
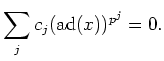
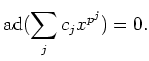
![]()