PROOF..
If
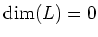
, then there is nothing to do.
We proceed by induction on
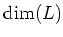
.
Let
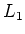
be a maximal among
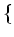
(Lie subalgebras of $L$ which is not equal to $L$)
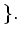
(The set above has a
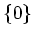
as a member, so it is not empty.)
In view of the lemma above, we see
We note that an vector space
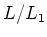
admits adjoint actions by
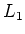
. Thus
That means,
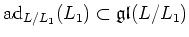
also satisfy the assumption of the theorem.
By the induction hypothesis, we see that conclusion (2) is
applicable to this case. Namely, there exists an element
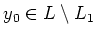
such that
holds.
Now a vector subset
of

is closed under Lie bracket and therefore it is a Lie subalgebra of

.
By the maximality of
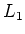
,
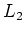
should equal to

. It is then also easy
to verify that
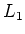
is an ideal of
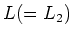
. This proves (1).
To prove (2), we note that 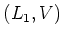 satisfies the assumption of the theorem.
So again by induction we see that
satisfies the assumption of the theorem.
So again by induction we see that 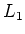 has a simultaneous 0
-eigen vector.
In other words,
has a simultaneous 0
-eigen vector.
In other words,
Let us then consider the action of
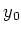
.
Thus
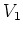
admits an action of
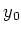
.
Since
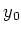
is nilpotent on
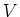
by the assumption, we see that
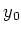
has
at least one 0
-eigen vector
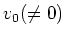
in
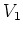
.
Then
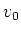
surely is a simultaneous 0
-eigen vector of

.
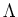
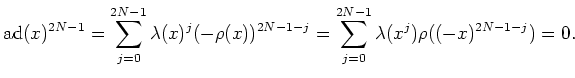
![]()
![]() satisfies the assumption of the theorem.
So again by induction we see that
satisfies the assumption of the theorem.
So again by induction we see that ![]() has a simultaneous 0
-eigen vector.
In other words,
has a simultaneous 0
-eigen vector.
In other words,
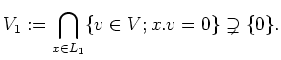
![]()
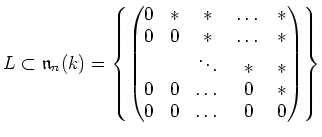
![]()