


Next: exterior derivation on 1-forms
Up: Topics in Non commutative
Previous: exterior algebras
Let 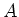 be a commutative ring. Let
be a commutative ring. Let 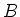 be a commutative
be a commutative 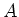 -algebra.
We have already defined the exterior derivation
-algebra.
We have already defined the exterior derivation
We define
2
We would like to extend this to a map
which satisfies the following rules.
|
(EXT1) |
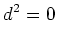 |
|
(EXT2) |
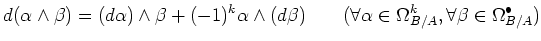 |
It is easy to see that 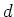 is uniquely determined by the
is uniquely determined by the
Subsections
2012-02-29
![]() is uniquely determined by the
is uniquely determined by the