There are a several equivalent ways to give a ``connection on
![]() ".
".
One way is to provide an isomorphism
such that
By the adjoint relation, we see that giving ![]() is equivalent
to giving an
is equivalent
to giving an
![]() -linear homomorphism
-linear homomorphism
such that the composition
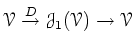
is equal to identity.
Now let us call
![]() ``the covariant derivation''.
Then
``the covariant derivation''.
Then ![]() is
is
![]() -linear homomorphism
-linear homomorphism
In terms of the covariant derivation
| (Co) |
Let us put it in terms of rings and modules.
Let
![]() and
and
![]() .
.
![]() be the defining
ideal of the diagonal
be the defining
ideal of the diagonal
![]() .
.
The
![]() -linear homomorphism
-linear homomorphism ![]() corresponds to a
corresponds to a ![]() -module homomorphism
-module homomorphism
such that
holds for all
Let us verify the identity (Co).