- free if it is isomorphic to a direct sum of
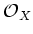 .
.
- locally free if there exists an open covering
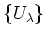 of
of 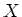 such that
such that
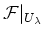 is free for all
is free for all 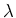 .
.
Such
Given a set of trivializations
![]() of
of
![]() , We notice that for any
, We notice that for any
![]() there exists a
there exists a
![]() -valued function
-valued function
such that for any section
We call