- If we are given a collection of continuous maps
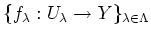 such that
such that
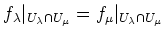
holds for any pair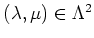 , then
we have a unique continuous map
, then
we have a unique continuous map 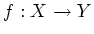 such that
such that
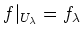
holds for any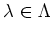 .
.
- Conversely, if we are given a continuous map
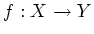 ,
then we obtain a collection of maps
,
then we obtain a collection of maps
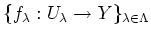 by restriction.
by restriction.