is equivalent to a data
which gives rise to a ring homomorphism
Let us take this homomorphism as
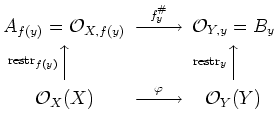
By the hypothesis of ![]() being a morphism of locally ringed spaces,
being a morphism of locally ringed spaces,
![]() is local homomorphism.
That means,
is local homomorphism.
That means,
From the definition of
We have thus proved that
![]() is equal to
is equal to ![]() as a map
as a map ![]() .
.
![]()