such that the following property holds.
- If there is another sheaf
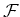 with a presheaf morphism
with a presheaf morphism
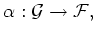
then there exists a unique sheaf homomorphism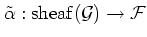
such that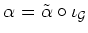
holds.
Furthermore, such
![]() is unique.
is unique.
such that the following property holds.
then there exists a unique sheaf homomorphism
such that
holds.
Furthermore, such
![]() is unique.
is unique.
The proof of Lemma 1.28 is divided in steps.
The first step is to know the uniqueness of such sheafification. It is most easily done by using universality arguments. ([1] has a short explanation on this topic.)
Then we divide the sheafification process in two steps.
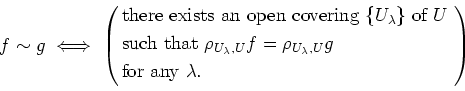
Then we define
Then
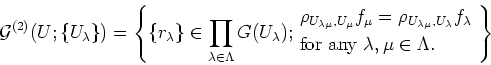
Then we define
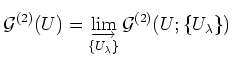
Then we may see that
Proofs of the above two lemma are routine work and are left to the reader.
Finish of the proof of Lemma 1.28: We put
ARRAY(0x92743dc)