

Next: ``Universal representation" of Weyl
Up: Representations of Weyl algebras
Previous: irreducible representations of the
PROOF..
Let
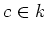
be an eigen value of
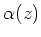
.
Then
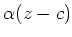
has a non trivial kernel. That means,
is a non zero vector subspace of
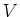
.
It is easy to verify that
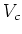
is a
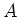
-submodule of
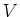
.
From the irreducibility assumption, we have
which in turn means that
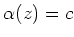
.
COROLLARY 7.8
Let 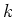 be an algebraically closed field of characteristic
be an algebraically closed field of characteristic 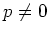 .
Then every finite dimensional irreducible representation
.
Then every finite dimensional irreducible representation
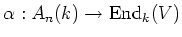 of
of 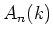 is equivalent to
a representation
is equivalent to
a representation 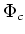 for some
for some
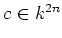 .
.
PROOF..
It is easy to see that
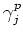
is in the center
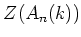
of the
Weyl algebra
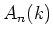
for
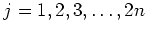
.
From the Lemma above, we have
for some
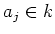
.
Let
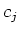
be the
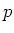
-th root of
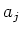
in
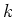
(which exists uniquely).
Then we see that
Thus
is essentially a representation of
.
For completeness's sake, we record here the following easy lemma.
PROOF..
Let us denote by
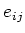
the
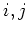
-elementary matrix.
That means,
Let
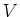
be the representation vector space.
We first note that
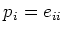
form a complete system
of mutually orthogonal projections.
That means,
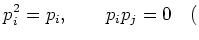
if
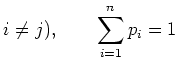
Let us thus put
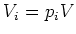
. Then we have
Furthermore,
is an isomorphism of vector space whose inverse is equal to
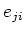
.
Let us take a linear basis
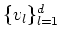 of
of 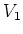 over
over 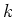 .
Then
.
Then
is a basis of
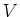
.
It is now easy to see that for each
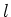
, the vector space
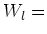
linear span
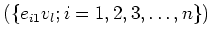
is isomorphic to the standard representation of
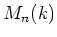
.
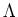
We also notice the following
COROLLARY 7.10
Let 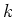 be a field of characteristic
be a field of characteristic 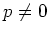 .
Then
.
Then
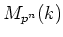 is generated by
is generated by
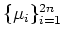 such that
such that
PROOF..
We take the representation
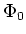
above and
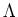


Next: ``Universal representation" of Weyl
Up: Representations of Weyl algebras
Previous: irreducible representations of the
2007-04-20
![]() the center
the center ![]() of
of ![]() ,
, ![]() is
equal to a constant.
is
equal to a constant.
![]() the center
the center ![]() of
of ![]() ,
, ![]() is
equal to a constant.
is
equal to a constant.
![]()
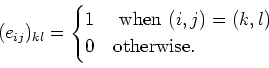
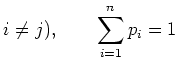
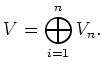
![]() of
of ![]() over
over ![]() .
Then
.
Then
![]()
![]()