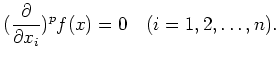
for any polynomial
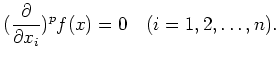
for any polynomial
Of course, differential operations give important examples of representation of the Weyl algebras.
Then we have
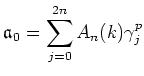
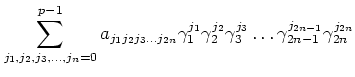
for some
To see the injectivity of
![]() ,
we employ a lexicographic order on
multi index sets and see that
,
we employ a lexicographic order on
multi index sets and see that
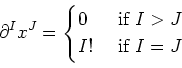
holds for any multi-indices
The surjectivity of
![]() is verified by counting dimensions.
is verified by counting dimensions.
![]()